
已知m,n表示两条不同直线,α表示平面.下列说法正确的是( )
A.若m∥α,n∥α,则m∥n
B.若m⊥α,n⊂α,则m⊥n
C.若m⊥α,m⊥n,则n∥α
D.若m∥α,m⊥n,则n⊥α
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案科目:高中数学 来源: 题型:
若点P是正四面体A BCD的面BCD上一点,且P到另外三个面的距离分别为h1,h2,h3,正四面体A BCD的高为h,则( )
A.h>h1+h2+h3
B.h=h1+h2+h3
C.h<h1+h2+h3
D.h1,h2,h3与h的关系不定
查看答案和解析>>
科目:高中数学 来源: 题型:
如图K411所示,正方形ACDE与等腰直角三角形
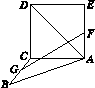
图K411
ACB所在的平面互相垂直,且AC=BC=2,∠ACB=90°,F,G分别是线段AE,BC的中点,则AD与GF所成的角的余弦值为( )
A.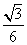 B.-
B.-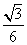
C.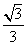 D.-
D.-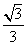
查看答案和解析>>
科目:高中数学 来源: 题型:
如图K40?8所示,某几何体的主视图和俯视图都是矩形,左视图是平行四边形,则该几何体的表面积为( )
A.15+3  B.9
B.9 
C.30+6  D.18
D.18 

图K40?8
查看答案和解析>>
科目:高中数学 来源: 题型:
已知四棱锥P ABCD的三视图如图K4014所示,其中主视图和左视图是直角三角形,俯视图是正方形,E是侧棱PC上的动点.
(1)求四棱锥P ABCD的体积.
(2)不论点E在何位置,是否都有BD⊥AE?证明你的结论.
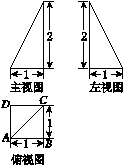
图K4014
查看答案和解析>>
科目:高中数学 来源: 题型:
下列结论中正确的有( )
(1)若直线上有无数个点不在平面内,则直线平行于这个平面;
(2)若一条直线与一个平面平行,则这条直线与这个平面内的所有直线都平行;
(3)两条平行线中的一条与一个平面平行,则另一条也和这个平面平行;
(4)若一条直线与一个平面相交,则平面内的所有直线均与该直线不平行.
A.0个 B.1个
C.2个 D.3个
查看答案和解析>>
科目:高中数学 来源: 题型:
如图K424所示,四棱锥P ABCD的底面是边长为a的正方形,侧棱PA⊥底面ABCD,BE⊥PC于点E,且BE= a,试在AB上找一点F,使EF∥平面PAD.
a,试在AB上找一点F,使EF∥平面PAD.
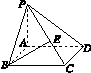
图K424
查看答案和解析>>
科目:高中数学 来源: 题型:
如图K438所示,三棱柱ABC A1B1C1的侧棱AA1⊥平面ABC,△ABC为等边三角形,侧面AA1C1C是正方形,E是A1B的中点,F是棱CC1上的点.
(1)若F是棱CC1的中点时,求证:AE⊥平面A1FB;
(2)当V三棱锥E ABF=9  时,求正方形AA1C1C的边长.
时,求正方形AA1C1C的边长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com