
分析 (1)令n=1,得a1=-k=2,即k=-2,再由an=Sn-Sn-1即可数列{an}的通项公式,再根据等比数列的求和公式求和即可,
(2)由bn=Tn-Tn-1,求出},{bn}的通项公式,根据{Cn}的通项公式可知利用由错位相减法能够求出数列{Cn}的前n项和Mn.
解答 解:(1)令n=1,得a1=-k=2,即k=-2,
∴Sn=2an-2,
当n≥2时,Sn-1=2an-1-2,
∴an=Sn-Sn-1=2an-2an-1,
∴an=2an-1,
∴数列{an}是以2为首项,2为公比的等比数列,所以{an}=2n,
∴Sn=2n+1-2
(2)∵等差数列{bn}的前n项和为Tn,且Tn=n2.
Tn-1=(n-1)2.
∴bn=Tn-Tn-1=2n-1,
∴cn=an•bn=(2n-1)2n,
∴数列{cn}的前n项和:
Mn=1×2+3×22+5×23+…+(2n-3)×2n-1+(2n-1)×2n,①
2Mn=1×22+3×23+5×24…+(2n-3)×2n+(2n-1)×2n+1,②
①-②,得-Mn=2+2×22+2×23+2×24+…+2×2n-(2n-1)×2n+1=2+2×$\frac{{2}^{2}-{2}^{n+1}}{1-2}$-(2m-1)×2n+1
即Mn=6+(2n-3)×2n+1.
点评 本题主要考查了数列的通项公式的求法和数列前n项和的求法,综合性强,难度大,易出错,属于中档题.


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,给出了一个算法框图,其作用是输入x的值,输出相应的y的值,若要使输入的x值与输出的y值相等,则这样的x的值有( )
如图,给出了一个算法框图,其作用是输入x的值,输出相应的y的值,若要使输入的x值与输出的y值相等,则这样的x的值有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
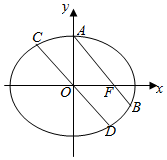 如图,点A,F分别是椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的上顶点和右焦点,过中心O作直线AF的平行线交椭圆于C,D两点,若CD的长是焦距的$\frac{{4\sqrt{5}}}{5}$倍,则该椭圆的离心率为$\frac{1}{2}$.
如图,点A,F分别是椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的上顶点和右焦点,过中心O作直线AF的平行线交椭圆于C,D两点,若CD的长是焦距的$\frac{{4\sqrt{5}}}{5}$倍,则该椭圆的离心率为$\frac{1}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com