练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】设，在复平面内z对应的点为Z，那么满足下列条件的点Z的集合是什么图形？

    （1）；

    （2）．

    【答案】（1）以原点O为圆心，以1为半径的圆．

    （2）以原点O为圆心，以1及2为半径的两个圆所夹的圆环，但不包括圆环的边界

    【解析】

    （1）根据复数模的定义确定复数对应点满足条件，即得轨迹；

    （2）根据复数模的定义确定复数对应点满足条件，即得轨迹.

    解：（1）由得，向量的模等于1，所以满足条件的点Z的集合是以原点O为圆心，以1为半径的圆．

    （2）不等式可化为不等式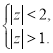

    不等式的解集是圆的内部所有的点组成的集合，不等式的解集是圆外部所有的点组成的集合，这两个集合的交集，就是上述不等式组的解集，也就是满足条件的点Z的集合．容易看出，所求的集合是以原点O为圆心，以1及2为半径的两个圆所夹的圆环，但不包括圆环的边界（如图）．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】选修4-4：坐标系与参数方程

    已知直线的参数方程为（为参数， ），以坐标原点为极点， 轴正半轴为极轴建立极坐标系，圆的极坐标方程为.

    （Ⅰ）讨论直线与圆的公共点个数；

    （Ⅱ）过极点作直线的垂线，垂足为，求点的轨迹与圆相交所得弦长.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知直线（为参数），曲线（为参数）.

    （1）设与相交于两点，求；

    （2）若把曲线上各点的横坐标压缩为原来的倍，纵坐标压缩为原来的倍，得到曲线，设点是曲线上的一个动点，求它到直线的距离的最大时，点P的坐标.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在考察黄烟经过药物处理和发生青花病的关系时，得到如下数据：在试验的470株黄烟中，经过药物处理的黄烟有25株发生青花病，60株没有发生青花病；未经过药物处理的有185株发生青花病，200株没有发生青花病．试推断药物处理跟发生青花病是否有关系．

    0.15

    0.10

    0.05

    0.025

    0.010

    0.005

    0.001

    2.072

    2.706

    3.841

    5.024

    6.635

    7.879

    10.828

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某城市有210家百货商店，其中大型商店20家，中型商店40家，小型商店150家.为了掌握各商店的营业情况，计划抽取一个容量为21的样本，应采用怎样的抽样方法？并写出抽样过程.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某技校开展技能大赛，甲、乙两班各选取5名学生加工某种零件，在4个小时内每名学生加工的合格零件数的统计数据的茎叶图如图所示，已知甲班学生在4个小时内加工的合格零件数的平均数为21，乙班学生在4个小时内加工的合格零件数的平均数不低于甲班的平均数.

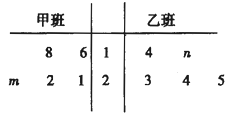
    （1）求的值；

    （2）分别求出甲、乙两班学生在4个小时内加工的合格零件数的方差和，并由此比较两班学生的加工水平的稳定性.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某公司为了解广告投入对销售收益的影响，在若干地区各投入万元广告费用，并将各地的销售收益绘制成频率分布直方图(如图所示).由于工作人员操作失误，横轴的数据丢失，但可以确定横轴是从开始计数的. [附：回归直线的斜率和截距的最小二乘估计公式分别为.]

    （1）根据频率分布直方图计算图中各小长方形的宽度;

    （2）试估计该公司投入万元广告费用之后，对应销售收益的平均值(以各组的区间中点值代表该组的取值);

    （3）该公司按照类似的研究方法,测得另外一些数据,并整理得到下表:

    广告投入 (单位:万元)

    1

    2

    3

    4

    5

    销售收益 (单位:万元)

    2

    3

    2

    7

    由表中的数据显示, 与之间存在着线性相关关系,请将（2）的结果填入空白栏,并求出关于的回归直线方程.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，点，直线，设圆的半径为1， 圆心在上.

    （1）若圆心也在直线上，过点作圆的切线，求切线方程；

    （2）若圆上存在点，使，求圆心的横坐标的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设定义在[﹣2，2]上的函数f（x）在区间[0，2]上单调递减，且f（1﹣m）＜f（3m）．

    （1）若函数f（x）在区间[﹣2，2]上是奇函数，求实数m的取值范围；

    （2）若函数f（x）在区间[﹣2，2]上是偶函数，求实数m的取值范围．

    查看答案和解析>>

    同步练习册答案