练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知在正项等比数列{an}中，a1=1，a2a4=16，则|a1﹣12|+|a2﹣12|+…+|a8﹣12|=（ ）
    A.224
    B.225
    C.226
    D.256

    【答案】B
    【解析】解：设正项等比数列{an}的公比为q＞0，∵a1=1，a2a4=16，∴q4=16，解得q=2．
    ∴ =2n﹣1 ，
    由2n﹣1≤12，解得n≤4．
    ∴|a1﹣12|+|a2﹣12|+…+|a8﹣12|=12﹣a1+12﹣a2+12﹣a3+12﹣a4+a5﹣12+…+a8﹣12
    =﹣2（a1+a2+a3+a4）+（a1+a2+…+a8）
    =﹣ +
    =﹣2（24﹣1）+28﹣1
    =225．
    故选B．
    【考点精析】关于本题考查的等比数列的通项公式（及其变式）和数列的前n项和，需要了解通项公式：；数列{an}的前n项和sn与通项an的关系才能得出正确答案．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】在△ABC中，内角A，B，C的对边分别为a，b，c．已知 ．
    （1）求 的值；
    （2）若cosB= ，△ABC的周长为5，求b的长．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为了在夏季降温和冬季供暖时减少能源损耗，房屋的屋顶和外墙需要建造隔热层．某幢建筑物要建造可使用20年的隔热层，每厘米厚的隔热层建造成本为6万元．该建筑物每年的能源消耗费用C（单位：万元）与隔热层厚度x（单位：cm）满足关系：C（x）= （0≤x≤10），若不建隔热层，每年能源消耗费用为8万元．设f（x）为隔热层建造费用与20年的能源消耗费用之和．
    （1）求k的值及f（x）的表达式．
    （2）隔热层修建多厚时，总费用f（x）达到最小，并求最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知点（1，2）是函数f（x）=ax（a＞0，且a≠1）的图象上一点，数列{an}的前n项和Sn=f（n）﹣1．
    求数列{an}的通项公式.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在边长为2的正方体ABCD﹣A1B1C1D1中，E是BC的中点，F是DD1的中点，
    （1）求点A到平面A1DE的距离；
    （2）求证：CF∥平面A1DE；
    （3）求二面角E﹣A1D﹣A的平面角大小的余弦值．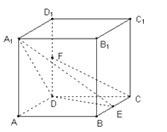

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为了迎接珠海作为全国文明城市的复查，爱卫会随机抽取了60位路人进行问卷调查，调查项目是自己对珠海各方面卫生情况的满意度（假设被问卷的路人回答是客观的），以分数表示问卷结果，并统计他们的问卷分数，把其中不低于50分的分成五段[50，60），[60，70），…[90，100]后画出如图部分频率分布直方图，观察图形信息，回答下列问题：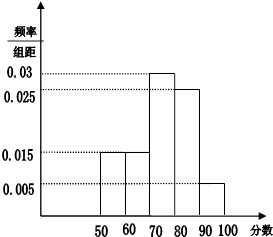

    （1）求出问卷调查分数低于50分的被问卷人数；
    （2）估计全市市民满意度在60分及以上的百分比．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数 ．

    （Ⅰ）若在上单调递减，求的取值范围；

    （Ⅱ）讨论的单调性．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）= 的定义域为集合A，B={x∈Z|2＜x＜10}，C={x∈R|x＜a或x＞a+1}
    （1）求A，（RA）∩B；
    （2）若A∪C=R，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为备战年瑞典乒乓球世界锦标赛，乒乓球队举行公开选拨赛，甲、乙、丙三名选手入围最终单打比赛名单.现甲、乙、丙三人进行队内单打对抗比赛，每两人比赛一场，共赛三场，每场比赛胜者得分，负者得分，在每一场比赛中，甲胜乙的概率为，丙胜甲的概率为，乙胜丙的概率为，且各场比赛结果互不影响.若甲获第一名且乙获第三名的概率为.

    （Ⅰ）求的值；

    （Ⅱ）设在该次对抗比赛中，丙得分为，求的分布列和数学期望.

    查看答案和解析>>

    同步练习册答案