
分析 先根据所围成图形的面积利用定积分表示出来,然后根据定积分的定义求出面积即可.
解答  解:∵曲线y=$\frac{1}{x}$和曲线y=x的交点为(1,1)与x=2的交点为(2,$\frac{1}{2}$),
解:∵曲线y=$\frac{1}{x}$和曲线y=x的交点为(1,1)与x=2的交点为(2,$\frac{1}{2}$),
∴y=$\frac{1}{x}$,y=x,x=2所围成图形的面积为
S=${∫}_{1}^{2}$(x-$\frac{1}{x}$)dx=($\frac{1}{2}{x}^{2}$-lnx)|${\;}_{1}^{2}$=2-ln2-$\frac{1}{2}$=$\frac{3}{2}$-ln2
故答案为:$\frac{3}{2}-ln2$
点评 本题主要考查了定积分在求面积中的应用,以及定积分的计算,属于基础题.


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | 不论采取哪种抽样方法,这100个零件中每个被抽到的概率都是$\frac{1}{5}$ | |
| B. | ①②两种抽样方法,这100个零件中每个被抽到的概率都是$\frac{1}{5}$,③并非如此 | |
| C. | ①③两种抽样方法,这100个零件中每个被抽到的概率都是$\frac{1}{5}$,②并非如此 | |
| D. | 采用不同的抽样方法,这100个零件中每个被抽到的概率各不相同 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 10 | B. | 9 | C. | 6 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
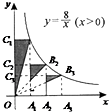 如图所示,点A1、A2、A3在x轴上,且OA1=A1A2=A2A3,分别过点A1、A2、A3作y轴的平行线,与反比例函数y=$\frac{8}{x}({x>0})$的图象分别交于点B1、B2、B3,分别过点B1,B2,B3作x轴的平行线,分别与y轴交于点C1,C2,C3,连接OB1,OB2,OB3,那么图中阴影部分的面积之和为$\frac{49}{9}$.
如图所示,点A1、A2、A3在x轴上,且OA1=A1A2=A2A3,分别过点A1、A2、A3作y轴的平行线,与反比例函数y=$\frac{8}{x}({x>0})$的图象分别交于点B1、B2、B3,分别过点B1,B2,B3作x轴的平行线,分别与y轴交于点C1,C2,C3,连接OB1,OB2,OB3,那么图中阴影部分的面积之和为$\frac{49}{9}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({0,\frac{1}{4}}]$ | B. | (0,1) | C. | $[{\frac{1}{4},1})$ | D. | (0,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 20名学生某次数学考试成绩(单位:分)的频率分布直方图如下:
20名学生某次数学考试成绩(单位:分)的频率分布直方图如下:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com