
 的定义域为R,且
的定义域为R,且 不为常函数,有以下命题:
不为常函数,有以下命题: 一定是偶函数;
一定是偶函数; 都有
都有 ,则
,则 是以2为周期的周期函数;
是以2为周期的周期函数; 是奇函数,且对任意
是奇函数,且对任意 都有
都有 ,则
,则 的图像关于直线
的图像关于直线 对称;
对称; ,且
,且 ,若
,若 恒成立,则
恒成立,则 为
为 上的增函数。
上的增函数。 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:不详 题型:解答题
 万元(
万元( )满足
)满足 (k为常数),如果不搞促销活动,则该产品的年销售量只能是1万件.已知2009年生产该产品的固定投入为8万元,每生产1万件该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品年平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金,不包括促销费用). (1)将2009年该产品的利润y万元表示为年促销费用
(k为常数),如果不搞促销活动,则该产品的年销售量只能是1万件.已知2009年生产该产品的固定投入为8万元,每生产1万件该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品年平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金,不包括促销费用). (1)将2009年该产品的利润y万元表示为年促销费用 万元的函数; (2)该厂家2009年的促销费用投入多少万元时,厂家的利润最大?
万元的函数; (2)该厂家2009年的促销费用投入多少万元时,厂家的利润最大?查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
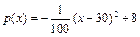 (万元),对开发的新产品,每年投入x万元,所获年利润为
(万元),对开发的新产品,每年投入x万元,所获年利润为
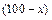 (万元),新产品开发用两年时间完成,这两年,每年从100万元生产准备资金中拿出80万元投入新产品开发,从第三年开始这100万元可随意分配且全部用于新旧产品的生产投入.为解决资金缺口,第一年初向银行贷款1000万元,年利率5.5%(不计复利,即先一年利息不计入下一年本金).(1)第五年底一次性向银行还本息多少万元?(2)从新产品开发的第三年起,新旧产品各投入多少万元年利润最大,最大利润是多少?(3)从新旧产品生产五年的最高利润总和中拿出70%来能否还清贷款?
(万元),新产品开发用两年时间完成,这两年,每年从100万元生产准备资金中拿出80万元投入新产品开发,从第三年开始这100万元可随意分配且全部用于新旧产品的生产投入.为解决资金缺口,第一年初向银行贷款1000万元,年利率5.5%(不计复利,即先一年利息不计入下一年本金).(1)第五年底一次性向银行还本息多少万元?(2)从新产品开发的第三年起,新旧产品各投入多少万元年利润最大,最大利润是多少?(3)从新旧产品生产五年的最高利润总和中拿出70%来能否还清贷款?查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.0 | B.-1 | C.0或-1 | D.0或1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com