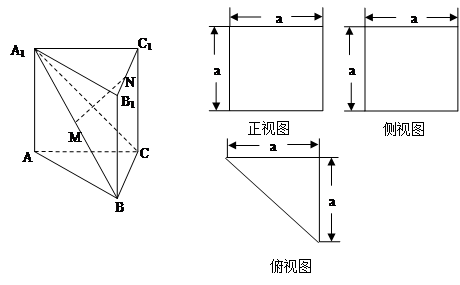试题分析:先由三视图还原几何体的直观图中线段长度,(1)利用直线与平面平行的判定定理,在平面内找一直线AC
1,由三角形中位线证明MN//AC
1,用直线与平面平行的判定定理得到结论;(2)通过证明平面内两相交直线同时垂直MN,由直线与平面垂直的判定定理得证.
试题解析:证明:由意可得:这个几何体是直三棱柱,
且AC^BC,AC=BC=CC
1 2分

(1)由直三棱柱的性质可得:AA
1^A
1B
1四边形ABCD为矩形,则M为AB
1的中点,N为B
1C
1的中点,在DAB
1C中,由中位线性质可得:
MN//AC
1,又AC
1Ì平面ACC
1A
1,MNË平面ACC
1A
1\ MN//平面ACC
1A
1 6分
(2)因为:CC
1^平面ABC,BCÌ平面ABC,\ CC
1^ BC,
又BC^AC,ACÇCC
1=C,所以,BC^平面ACC
1A
1,AC
1Ì平面ACC
1A
1\ BC^AC
1,在正方形ACC
1A
1中,AC
1^A
1C,BCÇA
1C=C,\ AC
1^平面A
1BC,
又AC
1//MN,\MN^平面A
1BC 10分