
��������������飺��ijУ�߶��꼶����15���࣬�ִ���ѡ��2���࣬������������״������ij���д��͡�������С�͵��̵깲1500�ң���������֮��Ϊ1��5��9��Ϊ�˵���ȫ���̵�ÿ�����۶��������ȡ����15�ҽ��е��飮��ɢ١�������������˲��õij������������ǣ� ��
A.��������������ֲ������
B.ϵͳ�������������������
C.�ֲ��������ϵͳ������
D.ϵͳ���������ֲ������
A
��������
�������������ٵ�����������࣬���Ҳ��첻���ϼ�������������÷�Χ����������д��͡�������С�͵��̵�ÿ�����۶���ڽϴ���죬���Ϸֲ���������÷�Χ
��������
��15������ѡ��2���࣬������������״����
����������࣬���Ҳ��첻��
�ʿɲ��ü���������ķ�����
1500�Ҵ��͡�������С�͵��̵��ÿ�����۶���ڽϴ���죬
�ʿɲ��÷ֲ�����ķ���
����ɢ١�������������˲��õij������������Ǽ�������������ֲ������
��ѡA



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��[ͬ��]2014����̰�ѡ��1-2 6.2��������ͼ��ϰ���������棩 ���ͣ�ѡ����
����ͼ������ͼ�����sΪ�� ��
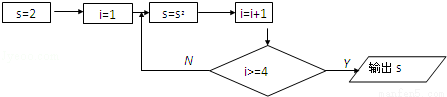
A.64 B.512 C.128 D.256
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��[ͬ��]2014����̰�ѡ��1-2 4.4һԪ���Իع鰸����ϰ���������棩 ���ͣ�?????
��2014•�Ƹ�ģ�⣩�Ѽ���������ر���X��Y��һ�����ݣ�xi��yi����i=1������n�������ع����֮��õ��ع�ֱ�߷�����б�ʵĹ���ֵΪ2���� ����ع�ֱ�߷���Ϊ�� ��
����ع�ֱ�߷���Ϊ�� ��
A.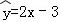 B.
B.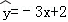 C.
C.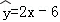 D.
D.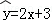
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��[ͬ��]2014����̰�ѡ��1-2 4.3�����������Է���������ϰ���������棩 ���ͣ�?????
��2014•��³ľ��һģ����ij�����ÿ���������Ŀ��ĸ���ΪP��0��P��1����ÿ������Ľ�����������������8������У���ǡ��3�λ���Ŀ�ꡱ�ĸ����ǡ�ǡ��5�λ���Ŀ�ꡱ�ĸ��ʵ�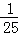 ����P��ֵΪ�� ��
����P��ֵΪ�� ��
A. B.
B. C.
C.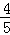 D.
D.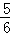
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��[ͬ��]2014����̰�ѡ��1-2 4.1�������ʵ�鰸����ϰ���������棩 ���ͣ�?????
ijѧУ����120̨���ԣ����м׳�24̨���ҳ�36̨������60̨�����ڴ����г�ȡһ����������Ϊ20����������ÿ�����屻�鵽�ĸ���Ϊ�� ��
A.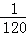 B.
B.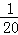 C.
C.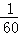 D.
D.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��[ͬ��]2014����̰�ѡ��1-2 4.1�������ʵ�鰸����ϰ���������棩 ���ͣ�?????
ijѧУ����������꼶ѧ����ɿκ���ҵ����ʱ�䣬��ȡ�����ֳ�������ķ�ʽ����һ����ѧ�����ͬѧ�����24��ͬѧ���е��飻�ڶ����ɽ����꼶��240��ѧ����ţ���001��240����ѧ�����һλΪ3��ͬѧ�μӵ��飬�������ֳ�����ʽ����Ϊ�� ��
A.�ֲ��������������� B.������������ֲ����
C.�ֲ������ϵͳ���� D.�����������ϵͳ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��[ͬ��]2014����̰�ѡ��1-2 4.1�������ʵ�鰸����ϰ���������棩 ���ͣ�?????
��2014•��ɽ��ģ���ü���������ķ����Ӻ���100����������������γ�ȡһ������Ϊ5�������������m���鵽�ĸ���Ϊ�� ��
A.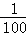 B.
B.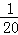 C.
C.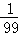 D.
D.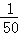
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��[ͬ��]2014����̰������ 12.2���ݱ�ʾ��������ȡ��ϰ���������棩 ���ͣ�?????
��2014•�㶫����֪ij������Сѧѧ���Ľ�������ֲ���ͼ1��ͼ2��ʾ��Ϊ�˽�õ�����Сѧ���Ľ����γ�ԭ���÷ֲ�����ķ�����ȡ2%��ѧ�����е��飬�����������ͳ�ȡ�ĸ��������������ֱ�Ϊ�� ��
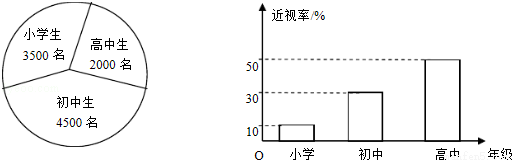
A.200��20 B.100��20 C.200��10 D.100��10
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��[ͬ��]2014����̰������ 7.4��������Ĵ����ⷨ��ϰ���������棩 ���ͣ�?????
��2014•ï��һģ����ֱ֪��l1��ax+2y+1=0��ֱ��l2����3��a��x��y+a=0����l1��l2����a��ֵΪ�� ��
A.1 B.2 C.6 D.1��2
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com