
【题目】已知命题P:4x﹣a2x+1≥0对x∈[﹣1,1]恒成立,命题Q:f(x)=log2(ax2﹣2x+ ![]() )的值域是R,若满足P且Q为假,P或Q为真,求实数a的取值范围.
)的值域是R,若满足P且Q为假,P或Q为真,求实数a的取值范围.
【答案】解:∵命题P:4x﹣a2x+1≥0对x∈[﹣1,1]恒成立,
∴a≤2x+2﹣x , 对x∈[﹣1,1]恒成立,
∴a≤2,
∵命题Q:f(x)=log2(ax2﹣2x+ ![]() )的值域是R,
)的值域是R,
∴①a=0时,f(x)=log2(﹣2x+ ![]() ),符合题意;
),符合题意;
②a≠0时,由题意,a>0且△≥0,
综上,0≤a≤3,
∵P且Q为假,P或Q为真,∴P、Q一真一假,
①若P真,Q假,则a<0;
②若P假,Q真,则2<a≤3.
综上,实数a的取值范围为(﹣∞,0)∪(2,3]
【解析】先解命题,再研究命题的关系.若p且q为假,p或q为真,两者是一真一假,计算可得答案.
【考点精析】利用复合命题的真假对题目进行判断即可得到答案,需要熟知“或”、 “且”、 “非”的真值判断:“非p”形式复合命题的真假与F的真假相反;“p且q”形式复合命题当P与q同为真时为真,其他情况时为假;“p或q”形式复合命题当p与q同为假时为假,其他情况时为真.


科目:高中数学 来源: 题型:
【题目】已知集合A={y|y=log2x,x≥4},B={y|y=( ![]() )x , ﹣1≤x≤0}.
)x , ﹣1≤x≤0}.
(1)求A∩B;
(2)若集合C={x|a≤x≤2a﹣1},且C∪B=B,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() 在
在![]() 单调递增,其中
单调递增,其中![]() .
.
(1)求![]() 的值;
的值;
(2)若![]() ,当
,当![]() 时,试比较
时,试比较![]() 与
与![]() 的大小关系(其中
的大小关系(其中![]() 是
是![]() 的导函数),请写出详细的推理过程;
的导函数),请写出详细的推理过程;
(3)当![]() 时,
时, ![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在空间直角坐标系中,已知A(3,0,1)和B(1,0,-3),试问
(1)在y轴上是否存在点M,满足 ![]() ?
?
(2)在y轴上是否存在点M,使△MAB为等边三角形?若存在,试求出点M坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
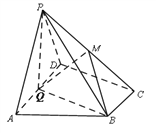
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为直角梯形,
为直角梯形, ![]() ,
, ![]() ,平面
,平面![]() 底面ABCD,Q为AD的中点,M是棱
底面ABCD,Q为AD的中点,M是棱![]() 上的点,
上的点, ![]()
(Ⅰ)若![]() 是棱
是棱![]() 的中点,求证:
的中点,求证: ![]() ;
;
(Ⅱ)若二面角![]() 的大小为
的大小为![]() ,试求
,试求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com