
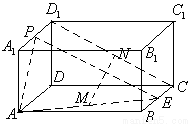
如图,在长方体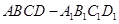 中,
中,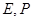 分别是
分别是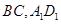 的中点,
的中点,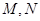 分
分
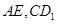 的中点,
的中点,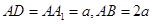
(Ⅰ)求证: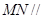 面
面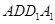 ;
;
(Ⅱ)求二面角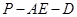 的大小。
的大小。
(Ⅲ)求三棱锥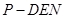 的体积。
的体积。
(Ⅰ)见解析;(Ⅱ)二面角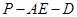 的余弦值为
的余弦值为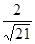 ;
;
(Ⅲ)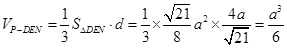 。
。
【解析】本试题主要是考查了立体几何中线面平行的证明,以及二面角的求解和锥体体积的计算的综合运用。
(1)利用线面平行的判定定理可知找到线线平行,从而得到结论。
(2)建立空间直角坐标系,然后表示平面的法向量,运用向量的夹角公式得到二面角的平面角的大小
(3)根据锥体体积的公式,利用底面积和高度来求解得到。
解:以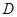 为原点,
为原点,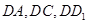 所在直线分别为
所在直线分别为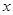 轴,
轴,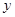 轴,
轴,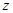 轴,建立直角坐标系,
轴,建立直角坐标系,
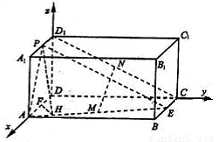
则: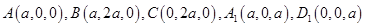
∵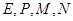 分别是
分别是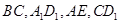 的中点
的中点
∴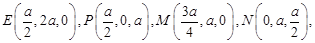
(Ⅰ)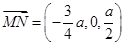
取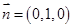 ,显然
,显然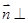 面
面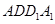
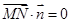 ,∴
,∴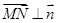
又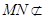 面
面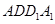 ∴
∴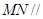 面
面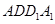 。。。。。。。。。。。
。。。。。。。。。。。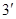
(Ⅱ)过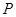 作
作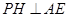 ,交
,交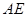 于
于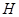 ,取
,取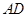 的中点
的中点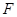 ,则
,则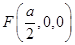 ∵
∵
设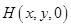 ,则
,则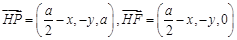
又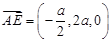
由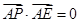 ,及
,及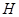 在直线
在直线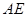 上,可得:
上,可得: 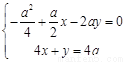
解得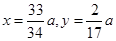
∴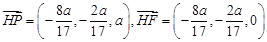 ∴
∴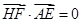 即
即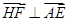
∴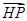 与
与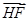 所夹的角等于二面角
所夹的角等于二面角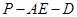 的大小
的大小
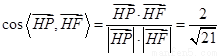
故:二面角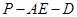 的余弦值为
的余弦值为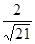 。。。。。
。。。。。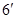
(Ⅲ)设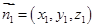 为平面
为平面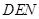 的法向量,则
的法向量,则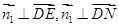
又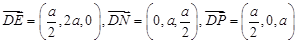
∴ 即
即 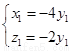 ∴可取
∴可取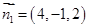
∴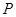 点到平面
点到平面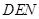 的距离为
的距离为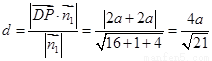
∵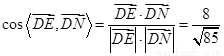 ,
, 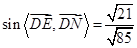
∴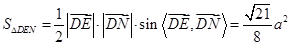
∴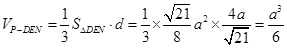 。。。。。。
。。。。。。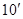


科目:高中数学 来源:2013-2014学年湖北武汉市高三2月调研测试文科数学试卷(解析版) 题型:选择题
如图,在长方体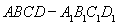 中,
中, 分别是棱
分别是棱 上的点(点
上的点(点 与
与 不重合),且
不重合),且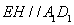 ,过
,过 的平面与棱
的平面与棱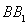 ,
,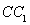 相交,交点分别为
相交,交点分别为 .设
.设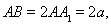
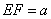 ,
, .在长方体
.在长方体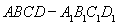 内随机选取一点,则该点取自于几何体
内随机选取一点,则该点取自于几何体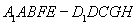 内的概率为( )
内的概率为( )

A.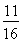 B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2011年浙江省高二上学期第一次统练试题理科数学 题型:解答题
(本题满分10分) 如图,在长方体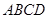 -
- 中,
中, 分别是
分别是 ,
,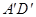 的中点,
的中点, 分别是
分别是 ,
, 中点,
中点,
(Ⅰ)求三棱锥 的体积;ks5u
的体积;ks5u
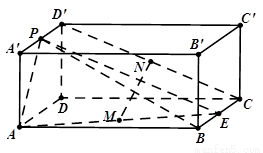
(Ⅱ)求证:
查看答案和解析>>
科目:高中数学 来源:2011年浙江省台州中学高二上学期第一次统练试题理科数学 题型:解答题
本题满分10分)如图,在长方体 -
- 中,
中, 分别是
分别是 ,
,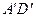 的中点,
的中点, 分别是
分别是 ,
,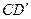 中点,
中点,

(Ⅰ)求三棱锥 的体积;
的体积;
(Ⅱ)求证:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com