
(本小题满分16分)已知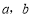 为实数,函数
为实数,函数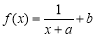 ,函数
,函数 .
.
(1)当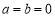 时,令
时,令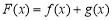 ,求函数
,求函数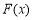 的极值;
的极值;
(2)当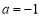 时,令
时,令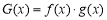 ,是否存在实数
,是否存在实数 ,使得对于函数
,使得对于函数 定义域中的任意实数
定义域中的任意实数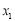 ,均存在实数
,均存在实数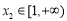 ,有
,有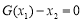 成立,若存在,求出实数
成立,若存在,求出实数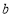 的取值集合;若不存在,请说明理由.
的取值集合;若不存在,请说明理由.
(1)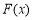 的极小值为
的极小值为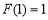 ,无极大值.(2)
,无极大值.(2)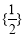
【解析】
试题分析:(1)当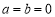 时,
时,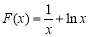 ,定义域为
,定义域为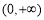 ,由
,由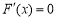 得
得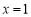 .列表分析得
.列表分析得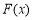 的极小值为
的极小值为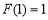 ,无极大值.(2)恒成立问题及存在问题,一般利用最值进行转化:
,无极大值.(2)恒成立问题及存在问题,一般利用最值进行转化: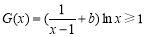 在
在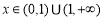 上恒成立.由于
上恒成立.由于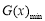 不易求,因此再进行转化:当
不易求,因此再进行转化:当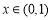 时,
时, 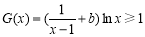 可化为
可化为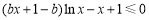 ,令
,令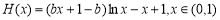 ,问题转化为:
,问题转化为: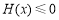 对任意
对任意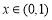 恒成立;同理当
恒成立;同理当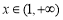 时,
时,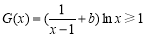 可化为
可化为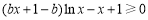 ,令
,令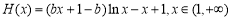 ,问题转化为:
,问题转化为: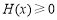 对任意的
对任意的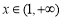 恒成立;以下根据导函数零点情况进行讨论即可.
恒成立;以下根据导函数零点情况进行讨论即可.
试题解析:(1)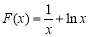 ,
,
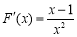 ,令
,令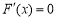 ,得
,得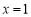 . 1分
. 1分
列表:
x |
|
|
|
|
| 0 | + |
| ↘ | 极小值 | ↗ |
所以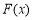 的极小值为
的极小值为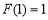 ,无极大值. 4分
,无极大值. 4分
(2)当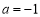 时,假设存在实数
时,假设存在实数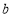 满足条件,则
满足条件,则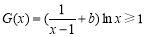 在
在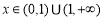 上恒成立. 5分
上恒成立. 5分
1)当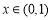 时,
时, 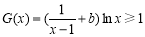 可化为
可化为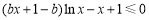 ,
,
令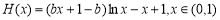 ,问题转化为:
,问题转化为: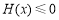 对任意
对任意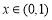 恒成立;(*)
恒成立;(*)
则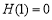 ,
,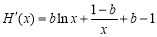 ,
,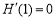 .
.
令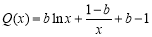 ,则
,则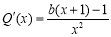 .
.
①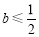 时,因为
时,因为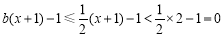 ,
,
故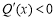 ,所以函数
,所以函数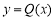 在
在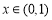 时单调递减,
时单调递减,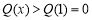 ,
,
即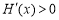 ,从而函数
,从而函数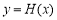 在
在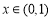 时单调递增,故
时单调递增,故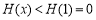 ,所以(*)
,所以(*)
成立,满足题意; 7分
②当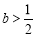 时,
时,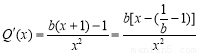 ,
,
因为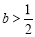 ,所以
,所以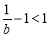 ,记
,记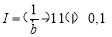 ,则当
,则当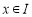 时,
时,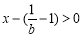 ,
,
故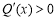 ,所以函数
,所以函数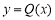 在
在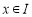 时单调递增,
时单调递增,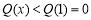 ,
,
即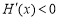 ,从而函数
,从而函数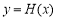 在
在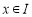 时单调递减,所以
时单调递减,所以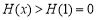 ,此时(*)不成立;
,此时(*)不成立;
所以当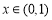 ,
,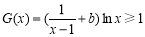 恒成立时,
恒成立时,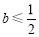 ; 9分
; 9分
2)当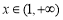 时,
时,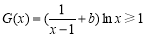 可化为
可化为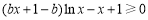 ,
,
令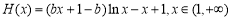 ,问题转化为:
,问题转化为: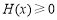 对任意的
对任意的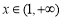 恒成立;(**)
恒成立;(**)
则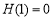 ,
,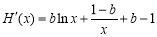 ,
,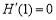 .
.
令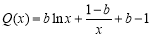 ,则
,则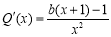 .
.
①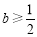 时,
时,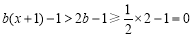 ,
,
故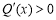 ,所以函数
,所以函数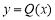 在
在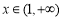 时单调递增,
时单调递增,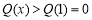 ,
,
即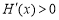 ,从而函数
,从而函数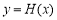 在
在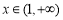 时单调递增,所以
时单调递增,所以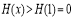 ,此时(**)成立;11分
,此时(**)成立;11分
②当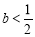 时,
时,
ⅰ)若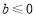 ,必有
,必有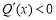 ,故函数
,故函数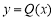 在
在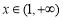 上单调递减,所以
上单调递减,所以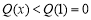 ,即
,即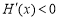 ,从而函数
,从而函数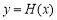 在
在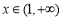 时单调递减,所以
时单调递减,所以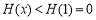 ,此时(**)不成立; 13分
,此时(**)不成立; 13分
ⅱ)若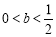 ,则
,则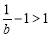 ,所以当
,所以当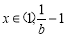 时,
时,
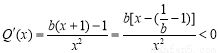 ,
,
故函数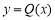 在
在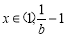 上单调递减,
上单调递减,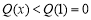 ,即
,即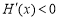 ,所以函数
,所以函数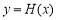 在
在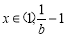 时单调递减,所以
时单调递减,所以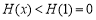 ,此时(**)不成立;
,此时(**)不成立;
所以当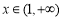 ,
,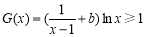 恒成立时,
恒成立时,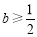 ; 15分
; 15分
综上所述,当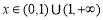 ,
,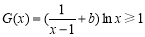 恒成立时,
恒成立时, 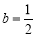 ,从而实数
,从而实数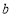 的取值集合为
的取值集合为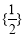 . 16分
. 16分
考点:利用导数求极值,利用导数研究函数单调性
考点分析: 考点1:导数及其应用 试题属性

 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案科目:高中数学 来源:2014-2015学年江苏省常州市高三上学期期末调研测试理科数学试卷(解析版) 题型:解答题
(本小题满分10分)一位网民在网上光顾某淘宝小店,经过一番浏览后,对该店铺中的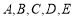 五种商品有购买意向.已知该网民购买
五种商品有购买意向.已知该网民购买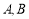 两种商品的概率均为
两种商品的概率均为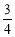 ,购买
,购买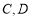 两种商品的概率均为
两种商品的概率均为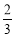 ,购买
,购买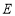 种商品的概率为
种商品的概率为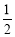 .假设该网民是否购买这五种商品相互独立.
.假设该网民是否购买这五种商品相互独立.
(1)求该网民至少购买4种商品的概率;
(2)用随机变量 表示该网民购买商品的种数,求
表示该网民购买商品的种数,求 的概率分布和数学期望.
的概率分布和数学期望.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年江苏省常州市高三上学期期末调研测试理科数学试卷(解析版) 题型:解答题
(本小题满分14分)在△ABC中,角A,B,C的对边分别为a,b,c.已知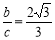 ,
,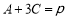 .
.
(1)求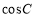 的值;(2)求
的值;(2)求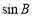 的值;(3)若
的值;(3)若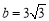 ,求△ABC的面积.
,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年贵州省贵阳市高三上学期期末监测考试文科数学试卷(解析版) 题型:填空题
题文已知全集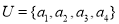 ,集合
,集合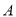 是集合
是集合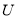 的恰有两个元素的子集,且满足下列三个条件:①若
的恰有两个元素的子集,且满足下列三个条件:①若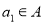 ,则
,则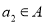 ;②若
;②若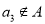 ,则
,则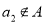 ;③若
;③若 ,则
,则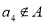 ,则集合
,则集合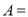 __________.(用列举法表示)
__________.(用列举法表示)
查看答案和解析>>
科目:高中数学 来源:2014-2015学年福建省龙岩市非一级达标校高三上学期期末检查文科数学试卷(解析版) 题型:解答题
(本小题满分12分)如图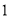 是图
是图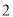 的三视图,三棱锥
的三视图,三棱锥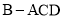 中,
中, ,
,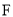 分别是棱
分别是棱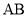 ,
, 的中点.
的中点.

(1)求证: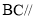 平面
平面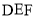 ;
;
(2)求三棱锥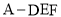 的体积.
的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com