
分析 根据“不等式ax2-bx+c>0的解集是(-1,2),”可判断a<0,-1,2,是ax2+bx+c=0的二根,从而可判断b,c的符号,问题即可解决.
解答 解:由题意可知:a<0,①错误,
-1,2是ax2-bx+c=0的二根,∴-1+2=1=$\frac{b}{a}$,-1×2=$\frac{c}{a}$,∴b=a,c=-2a,∴b<0,c>0,∴②正确,
令f(x)=ax2-bx+c,由题意可知f(1)=a+b+c>0,∴③错误,
f(-1)=a+b+c=0,∴④错误,
∵ax2+bx+c=0,设其两根为x1,x2,
∴x1+x2=-$\frac{b}{a}$=-1,x1•x2=$\frac{c}{a}$=-2,
∴不等式ax2+bx+c>0的解集是(-2,-1),∴⑤错误,
故答案为:②
点评 本题考查一元二次不等式的应用,着重考查三个“二次”(二次函数y=ax2+bx+c(a≠0),一元二次不等式,一元二次方程ax2+bx+c=0(a≠0)))之间的关系,属于中档题.


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案科目:高中数学 来源:2017届江西南昌新课标高三一轮复习训练三数学试卷(解析版) 题型:解答题
已知函数 (
( 为常数,
为常数,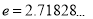 是自然对数的底数),曲线
是自然对数的底数),曲线 在点
在点 处的切线与
处的切线与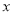 轴平行.
轴平行.
(1)求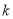 的值;
的值;
(2)求 的单调区间;
的单调区间;
(3)设 ,其中
,其中 为
为 的导函数.证明:对任意
的导函数.证明:对任意 ,
,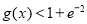 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com