
【题目】已知函数![]() ,若关于x的方程
,若关于x的方程![]() 有四个不等实根,且
有四个不等实根,且![]() 恒成立,则实数
恒成立,则实数![]() 的最小值为________.
的最小值为________.
【答案】![]()
【解析】
函数![]() 是分段函数,通过求导分析得到函数
是分段函数,通过求导分析得到函数![]() 在
在![]() 上为增函数,在
上为增函数,在![]() 上为增函数,在
上为增函数,在![]() 上为减函数,求得函数
上为减函数,求得函数![]() 在
在![]() 上,当
上,当![]() 时有一个极大值1,所以要使方程
时有一个极大值1,所以要使方程![]() 有四个实数根,
有四个实数根,![]() 的值一个要在
的值一个要在![]() 内,一个在
内,一个在![]() 内,然后运用二次函数的图象及二次方程根的关系列式求解
内,然后运用二次函数的图象及二次方程根的关系列式求解![]() 和
和![]() 的取值范围,从而求出
的取值范围,从而求出![]() 的最小值.
的最小值.
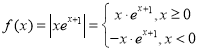 ,
,
当![]() 时,
时,![]() 恒成立,所以
恒成立,所以![]() 在
在![]() 上为增函数,
上为增函数,
当![]() 时,
时,![]() ,
,
由![]() ,得
,得![]() ,当
,当![]() 时,
时,![]() ,
,![]() 为增函数,
为增函数,
当![]() 时,
时,![]() ,
,![]() 为减函数,
为减函数,
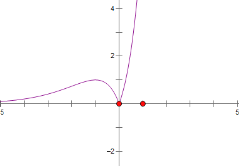
所以函数![]() 的极大值为
的极大值为![]() ,
,
极小值为:![]() ,如图:
,如图:
令![]() ,由韦达定理得:
,由韦达定理得:![]() ,
,![]() ,
,
(1)因为当![]() ,且
,且![]() 时,方程
时,方程![]() 没有实根,故舍去.
没有实根,故舍去.
(2)又当![]() ,且
,且![]() (不妨设),由图象可得
(不妨设),由图象可得![]() 至多有三个实根,
至多有三个实根,
由此可得方程![]() 至多有三个实根,不符合题意.
至多有三个实根,不符合题意.
(3)若![]() 是方程
是方程![]() 的根,代入可得
的根,代入可得![]() ,所以
,所以![]() ,解得
,解得![]() ,而根据图象可知
,而根据图象可知![]() 无解,
无解,![]() 和
和![]() 都只有一个根,不符合题意.
都只有一个根,不符合题意.
故要使方程![]() 有四个不等实数根,
有四个不等实数根,
则方程![]() 应有两个不相同的正实根,
应有两个不相同的正实根,
即![]() ,且
,且![]() ,此时
,此时![]() ,且一个根在
,且一个根在![]() 内,一个根在
内,一个根在![]() 内,
内,
再令![]() ,
,
因为![]() ,①
,①![]() ,
,
则![]() ,②
,②
则只需![]() ,即
,即![]() ,
,
所以![]() ,③
,③
将③式平方可得:![]() ,④
,④
由①②解得:![]() ,⑤
,⑤
由④得到:![]() ,由④⑤得到:
,由④⑤得到:![]() ,
,
所以![]() ,
,![]() .
.
所以本题答案为![]() .
.


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:高中数学 来源: 题型:
【题目】我市准备实施天然气价格阶梯制,现提前调查市民对天然气价格阶梯制的态度,随机抽查了![]() 名市民,现将调查情况整理成了被调查者的频率分布直方图(如图)和赞成者的频数表如下:
名市民,现将调查情况整理成了被调查者的频率分布直方图(如图)和赞成者的频数表如下:
年龄(岁) |
|
|
|
|
|
|
赞成人数 |
|
|
|
|
|
|
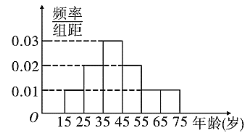
(1)若从年龄在![]() ,
,![]() 的被调查者中各随机选取
的被调查者中各随机选取![]() 人进行调查,求所选取的
人进行调查,求所选取的![]() 人中至少有
人中至少有![]() 人对天然气价格阶梯制持赞成态度的概率;
人对天然气价格阶梯制持赞成态度的概率;
(2)若从年龄在![]() ,
,![]() 的被调查者中各随机选取
的被调查者中各随机选取![]() 人进行调查,记选取的
人进行调查,记选取的![]() 人中对天然气价格实施阶梯制持不赞成态度的人数为
人中对天然气价格实施阶梯制持不赞成态度的人数为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一次田径比赛中,35名运动员的成绩(单位:分钟)的茎叶图如图所示。

若将运动员按成绩由好到差编为1—35号,再用系统抽样方法从中抽取5人,则其中成绩在区间![]() 上的运动员人数为
上的运动员人数为
A.6B.5C.4D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的部分图象如图所示:
的部分图象如图所示:

(I)求![]() 的解析式及对称中心坐标;
的解析式及对称中心坐标;
(Ⅱ)将![]() 的图象向右平移
的图象向右平移![]() 个单位,再将横坐标伸长到原来的2倍,纵坐标不变,最后将图象向上平移1个单位,得到函数
个单位,再将横坐标伸长到原来的2倍,纵坐标不变,最后将图象向上平移1个单位,得到函数![]() 的图象,求函数
的图象,求函数![]() 在
在![]() 上的单调区间及最值.
上的单调区间及最值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三棱锥P﹣ABC中,AC⊥BC,AC=BC=2,PA=PB=PC=3,O是AB中点,E是PB中点.
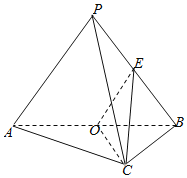
(1)证明:平面PAB⊥平面ABC;
(2)求点B到平面OEC的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业有甲、乙两套设备生产同一种产品,为了检测两套设备的生产质量情况,随机从两套设备生产的大量产品中各抽取了50件产品作为样本,检测一项质量指标值,若该项质量指标值落在![]() 内,则为合格品,否则为不合格品.表1是甲套设备的样本的频数分布表,图1是乙套设备的样本的频率分布直方图.
内,则为合格品,否则为不合格品.表1是甲套设备的样本的频数分布表,图1是乙套设备的样本的频率分布直方图.
表1:甲套设备的样本的频数分布表
质量指标值 |
|
|
|
|
|
|
频数 | 1 | 5 | 18 | 19 | 6 | 1 |
图1:乙套设备的样本的频率分布直方图
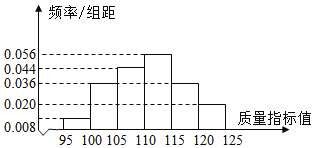
(1)根据表1和图1,通过计算合格率对两套设备的优劣进行比较;
(2)填写下面列联表,并根据列联表判断是否有![]() 的把握认为该企业生产的这种产品的质量指标值与甲、乙两套设备的选择有关.
的把握认为该企业生产的这种产品的质量指标值与甲、乙两套设备的选择有关.
甲套设备 | 乙套设备 | 合计 | |
合格品 | |||
不合格品 | |||
合计 |
附:
| 0.15 | 0.10 | 0.050 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
参考公式: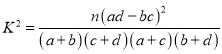 ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() ,
,![]() 为自然对数的底数).
为自然对数的底数).
(1)若曲线![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 垂直,求
垂直,求![]() 的单调区间;
的单调区间;
(2)若函数![]() 有两个极值点,求实数
有两个极值点,求实数![]() 的取值范围;
的取值范围;
(3)证明:当![]() 时,
时,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com