练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    14．若C${\;}_{21}^{k-4}$＜C${\;}_{21}^{k-2}$＜C${\;}_{21}^{k-1}$（k∈N），则k的取值范围是（　　）
    A．[5，11]B．[4，11]C．[4，12]D．[4，15]

    分析 直接利用组合数公式化简不等式求解即可．

    解答 解：C${\;}_{21}^{k-4}$＜C${\;}_{21}^{k-2}$＜C${\;}_{21}^{k-1}$（k∈N），
    可得$\frac{21!}{（k-4）!（25-k）!}＜\frac{21!}{（k-2）!（23-k）!}＜\frac{21!}{（k-1）!（22-k）!}$，k-4≥0，
    即$\frac{1}{（25-k）（24-k）}＜\frac{1}{（k-2）（k-3）}$并且$\frac{1}{23-k}＜\frac{1}{k-1}$，
    解得：4≤k＜12．
    k的取值范围是[4，11]．
    故选：B．

    点评 本题考查组合数公式的应用，不等式组的解法，考查计算能力．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    4．已知$\overrightarrow{m}$=（sin（2α+β），cosβ），$\overrightarrow{n}$=（cos（2α-β），sinβ），且$\overrightarrow{m}$∥$\overrightarrow{n}$，则锐角α，β的值为（　　）
    A．α=$\frac{π}{4}$，β任意B．α任意，β=$\frac{π}{4}$C．α=β=$\frac{π}{4}$D．α任意，β任意

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

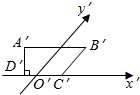    5．如图所示，A′B′C′D′是一个水平放置的平面图形的斜二测直观图，已知A′B′C′D′是一个直角梯形，A′B′∥C′D′，A′D′⊥C′D′，且B′C′与y轴平行，又A′B′=21，DC′′=9，A′D′=12，试求梯形A′B′C′D′的原图形ABCD的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    2．已知函数f（x）=（2x+a）2，若f（x）在x=a处的导数值为20，则a=$\frac{5}{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    9．若y=$\frac{ax+b}{{x}^{2}+1}$的值域[-1，4]，求a，b的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    19．在一次青年歌手大奖赛中，七位评委为某参赛选手打出的分数的茎叶图如图所示，去掉一个最高分和一个最低分，所剩数据的平均值为83．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    6．如图，在长方体ABCD-A1B1C1D1中，求证：面AA1D1D∥面BB1C1C．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．设函数y=|ex-1|的图象与直线y=$\frac{1}{m+1}$的两交点横坐标分别为x1、x2（x1＜x2），与直线y=m的两交点横坐标分别为x3、x4（x3＜x4），若m∈（0，$\frac{1}{2}$），则（x4+x1）-（x3+x2）的取值范围是（　　）
    A．（-∞，0）B．（-∞，ln$\frac{3}{5}$）C．（ln$\frac{3}{5}$，0）D．（-∞，-1）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．设全集U={3，6，m2-m-1}，A={|3-2m|，6}，∁UA={5}，求实数m．

    查看答案和解析>>

    同步练习册答案