Question

17．已知函数$f（x）=cos[{\frac{π}{2}（1-x）}]$，任意的t∈R，记函数f（x）在区间[t，t+1]上的最大值为M（t），最小值为m（t），则函数h（t）=M（t）-m（t）的值域为$[{1-\frac{{\sqrt{2}}}{2}，\sqrt{2}}]$．

Answer 1

分析 利用正弦函数的周期公式可得其周期T=4，区间[t，t+1]的长度为$\frac{1}{4}$T，利用正弦函数的图象与性质，可求得函数h（t）=M（t）-m（t）的值域．

解答 解：∵$f（x）=cos[{\frac{π}{2}（1-x）}]$=sin$\frac{π}{2}$x，
∴其周期T=4，区间[t，t+1]的长度为$\frac{1}{4}$T，
又f（x）在区间[t，t+1]上的最大值为M_t，最小值为m_t，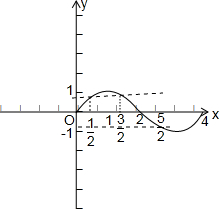

由正弦函数的图象与性质可知，当x∈[4k+$\frac{1}{2}$，4k+$\frac{3}{2}$]时，h（t）=M（t）-m（t），取得最小值1-$\frac{\sqrt{2}}{2}$；
当x∈[4k+$\frac{3}{2}$，4k+$\frac{5}{4}$]时，h（t）=M（t）-m（t）取得最大值$\frac{\sqrt{2}}{2}$-（-$\frac{\sqrt{2}}{2}$）=$\sqrt{2}$；
∴函数h（t）的值域为$[{1-\frac{{\sqrt{2}}}{2}，\sqrt{2}}]$．
故答案为$[{1-\frac{{\sqrt{2}}}{2}，\sqrt{2}}]$．

点评 本题考查正弦函数的周期性、单调性与最值，考查分析问题，解决问题的能力，属于中档题．