练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知函数f(x)＝4cosωx·sin(ωx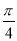＋)(ω>0)的最小正周期为π．

    (1)求ω的值；

    (2)讨论f(x)在区间[0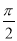，]上的单调性．

     

    （1）ω＝1

    （2）f(x)在区间[0，]上单调递增，在区间[，]上单调递减．

    【解析】【解析】
    (1)f(x)＝4cosωx·sin(ωx＋)

    ＝2sinωx·cosωx＋2cos2ωx

    ＝ (sin2ωx＋cos2ωx)＋

    ＝2sin(2ωx＋)＋．

    ∵f(x)的最小正周期为π，且ω>0，

    从而有＝π，故ω＝1．

    (2)由(1)知f(x)＝2sin(2x＋)＋．

    若0≤x≤，则≤2x＋≤．

    当≤2x＋≤，即0≤x≤时，f(x)单调递增；

    当≤2x＋≤，即≤x≤时，f(x)单调递减．

    综上可知，f(x)在区间[0，]上单调递增，在区间[，]上单调递减．

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：4-2平面向量的基本定理及坐标表示（解析版） 题型：选择题

    已知向量a＝(2,1)，b＝(1，k)，且a与b的夹角为锐角，则实数k的取值范围是(　　)

    A．(－2，＋∞) B．(－2，)∪(，＋∞)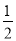

    C．(－∞，－2) D．(－2,2)

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：3-7正弦定理和余弦定理（解析版） 题型：解答题

    在△ABC中，a，b，c分别是三内角A，B，C所对的三边，已知b2＋c2＝a2＋bc．

    (1)求角A的大小；

    (2)若2sin2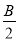＋2sin2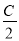＝1，试判断△ABC的形状．

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：3-6简单的三角恒等变换（解析版） 题型：填空题

    设α，β∈(0，π)，且sin(α＋β)＝，tan＝，则cosβ的值为________．

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：3-6简单的三角恒等变换（解析版） 题型：选择题

    ＝(　　)

    A．－ B． C． D．1

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：3-5两角和与差的正弦、余弦和正切（解析版） 题型：填空题

    已知α为锐角，且cos(α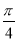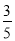＋)＝，则sinα＝________．

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：3-4正弦型函数的图象及应用（解析版） 题型：解答题

    已知函数f(x)＝Asin(2x＋θ)，其中A≠0，θ∈(0，)．

    (1)若函数f(x)的图象过点E(－，1)，F(，)，求函数f(x)的解析式；

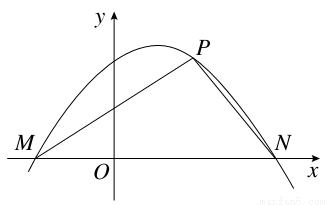
    (2)如图，点M，N是函数y＝f(x)的图象在y轴两侧与x轴的两个相邻交点，函数图象上一点P(t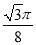，)满足·＝，求函数f(x)的最大值．

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：3-3三角函数的图象与性质（解析版） 题型：选择题

    设函数f(x)＝|sin(2x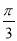＋)|，则下列关于函数f(x)的说法中正确的是(　　)

    A．f(x)是偶函数

    B．f(x)的最小正周期为π

    C．f(x)的图象关于点(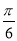－，0)对称

    D．f(x)在区间[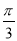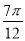，]上是增函数

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：2-8函数与方程（解析版） 题型：选择题

    函数f(x)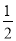＝()x－sinx在区间[0,2π]上的零点个数为(　　)

    A．1 B．2 C．3 D．4

     

    查看答案和解析>>

    同步练习册答案