
【题目】如图,在四棱锥P—ABCD中,平面PAD⊥底面ABCD,其中底面ABCD为等腰梯形,AD∥BC,PA=AB=BC=CD=2,PD=2![]() ,PA⊥PD,Q为PD的中点.
,PA⊥PD,Q为PD的中点.
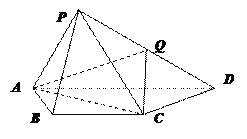
(Ⅰ)证明:CQ∥平面PAB;
(Ⅱ)求直线PD与平面AQC所成角的正弦值.
【答案】(Ⅰ)见解析;(Ⅱ) ![]() .
.
【解析】试题分析:
(1) 取PA的中点N,由题意证得BN∥CQ,则CQ∥平面PAB.
(2)利用题意建立空间直角坐标系,结合平面的法向量可得直线PD与平面AQC所成角的正弦值为![]() .
.
试题解析:
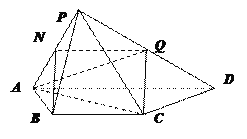
(Ⅰ)证明 如图所示,取PA的中点N,连接QN,
BN.在△PAD中,PN=NA,PQ=QD,
所以QN∥AD,且QN=![]() AD.
AD.
在△APD中,PA=2,PD=2![]() ,PA⊥PD,
,PA⊥PD,
所以AD=![]() =4,而BC=2,所以BC=
=4,而BC=2,所以BC=![]() AD.
AD.
又BC∥AD,所以QN∥BC,且QN=BC,
故四边形BCQN为平行四边形,所以BN∥CQ.
又BN平面PAB,且CQ![]() 平面PAB, 所以CQ∥平面PAB.
平面PAB, 所以CQ∥平面PAB.
(Ⅱ)如图,取AD的中点M,连接BM;取BM的中点O,连接BO、PO.
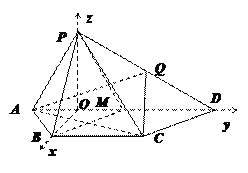
由(1)知PA=AM=PM=2,
所以△APM为等边三角形,
所以PO⊥AM. 同理BO⊥AM.
因为平面PAD⊥平面ABCD,所以PO⊥BO.
如图,以O为坐标原点,分别以OB,OD,OP所在直线为x轴,y轴,z轴建立空间直角坐标系,则O(0,0,0),D(0,3,0),A(0,-1,0),B(![]() ,0,0),P(0,0,
,0,0),P(0,0,![]() ),C(
),C(![]() ,2,0),
,2,0),
则![]() =(
=(![]() ,3,0).
,3,0).
因为Q为DP的中点,故Q![]() ,所以
,所以![]() =
=![]() .
.
设平面AQC的法向量为m=(x,y
则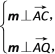 可得
可得
令y=-![]() ,则x=3,z=5. 故平面AQC的一个法向量为m=(3,-
,则x=3,z=5. 故平面AQC的一个法向量为m=(3,-![]() ,5).
,5).
设直线PD与平面AQC所成角为θ.
则sinθ= |cos〈![]() ,m〉|=
,m〉|=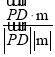 =
=![]() .
.
从而可知直线PD与平面AQC所成角正弦值为![]() .
.


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:高中数学 来源: 题型:
【题目】在物理实验中,为了研究所挂物体的重量x对弹簧长度y的影响.某学生通过实验测量得到物体的重量与弹簧长度的对比表:
物体重量(单位g) | 1 | 2 | 3 | 4 | 5 |
弹簧长度(单位cm) | 1.5 | 3 | 4 | 5 | 6.5 |
参考公式:
①.样本数据x1 , x2 , …xn的标准差
s= ![]() ,其中
,其中 ![]() 为样本的平均数;
为样本的平均数;
②.线性回归方程系数公式 ![]() =
= 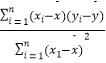 =
= 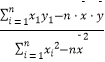 ,
, ![]() =
= ![]() ﹣
﹣ ![]()
![]() .
.
(1)画出散点图;
(2)利用所给的参考公式,求y对x的回归直线方程;
(3)预测所挂物体重量为8g时的弹簧长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校在一次趣味运动会的颁奖仪式上,高一、高二、高三各代表队人数分别为120人、120人、n人.为了活跃气氛,大会组委会在颁奖过程中穿插抽奖活动,并用分层抽样的方法从三个代表队中共抽取20人在前排就坐,其中高二代表队有6人. 
(1)求n的值;
(2)把在前排就坐的高二代表队6人分别记为a,b,c,d,e,f,现随机从中抽取2人上台抽奖.求a和b至少有一人上台抽奖的概率.
(3)抽奖活动的规则是:代表通过操作按键使电脑自动产生两个[0,1]之间的均匀随机数x,y,并按如图所示的程序框图执行.若电脑显示“中奖”,则该代表中奖;若电脑显示“谢谢”,则不中奖,求该代表中奖的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,已知点A(1,0),D(﹣1,0),点B,C在单位圆O上,且∠BOC= ![]() .
. 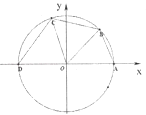
(Ⅰ)若点B( ![]() ,
, ![]() ),求cos∠AOC的值;
),求cos∠AOC的值;
(Ⅱ)设∠AOB=x(0<x< ![]() ),四边形ABCD的周长为y,将y表示成x的函数,并求出y的最大值.
),四边形ABCD的周长为y,将y表示成x的函数,并求出y的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,底面ABCD为正方形,平面PAD⊥平面ABCD,点M在线段PB上,PD//平面MAC,PA=PD=![]() ,AB=4.
,AB=4.
(I)求证:M为PB的中点;
(II)求二面角B-PD-A的大小;
(III)求直线MC与平面BDP所成角的正弦值.
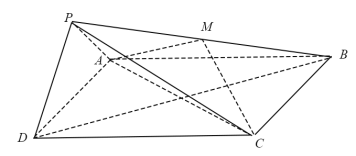
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+2bx+c,且f(1)=f(3)=﹣1.设a>0,将函数f(x)的图像先向右平移a个单位长度,再向下平移a2个单位长度,得到函数g(x)的图像. (Ⅰ)若函数g(x)有两个零点x1 , x2 , 且x1<4<x2 , 求实数a的取值范围;
(Ⅱ)设连续函数在区间[m,n]上的值域为[λ,μ],若有 ![]() ,则称该函数为“陡峭函数”.若函数g(x)在区间[a,2a]上为“陡峭函数”,求实数a的取值范围.
,则称该函数为“陡峭函数”.若函数g(x)在区间[a,2a]上为“陡峭函数”,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
, ![]() ,
, ![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)记 ,设
,设![]() ,
, ![]() 为函数
为函数![]() 图象上的两点,且
图象上的两点,且![]() .
.
(ⅰ)当![]() ,
, ![]() 时,若
时,若![]() 在
在![]() 处的切线相互垂直,求证:
处的切线相互垂直,求证: ![]() ;
;
(ⅱ)若![]() 在点
在点![]() 处的切线重合,求
处的切线重合,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com