
【题目】已知函数![]()
(![]() )当
)当![]() 时,求
时,求![]() 的单调区间和极值.
的单调区间和极值.
(![]() )若对于任意
)若对于任意![]() ,都有
,都有![]() 成立,求
成立,求![]() 的取值范围 ;
的取值范围 ;
(![]() )若
)若![]() 且
且![]() 证明:
证明:![]()
【答案】⑴详见解析;⑵详见解析.
【解析】试题分析:(1)求导数![]() 分类讨论①
分类讨论①![]() 时,
时,![]() ②当
②当![]() 时,令
时,令![]() 解得
解得![]() ,当
,当![]() 时,
时,![]() 当
当![]() 写出单调区间及极值.
写出单调区间及极值.
(2)转化为![]() 对于
对于![]() 恒成立.分离参数
恒成立.分离参数![]() 对于
对于![]() 恒成立,利用导数求不等式右边的最大值即可.
恒成立,利用导数求不等式右边的最大值即可.
(3)不妨设![]() 则
则![]() ,要证
,要证![]() 只要证
只要证![]() 即证
即证![]() 因为
因为![]() 在区间
在区间![]() 上单调递增,所以
上单调递增,所以![]()
又![]() 即证
即证![]() 构造函数
构造函数![]() 函数
函数![]() 在区间
在区间![]() 上单调递增,故
上单调递增,故![]() 而
而![]() 故
故![]()
所以![]() 即
即![]() 所以
所以![]() 成立.
成立.
试题解析:⑴ ![]()
①![]() 时,因为
时,因为![]() 所以
所以![]()
函数![]() 的单调递增区间是
的单调递增区间是![]() ,无单调递减区间,无极值;
,无单调递减区间,无极值;
②当![]() 时,令
时,令![]() 解得
解得![]() ,
,
当![]() 时,
时,![]() 当
当![]()
所以函数![]() 的单调递减区间是
的单调递减区间是![]() ,单调递增区间是
,单调递增区间是![]() ,
,
在区间![]() 上的极小值为
上的极小值为![]() 无极大值.
无极大值.
⑵ 由题意,![]()
即问题转化为![]() 对于
对于![]() 恒成立.
恒成立.
即![]() 对于
对于![]() 恒成立,
恒成立,
令![]() ,则
,则![]()
令![]() ,则
,则![]()
所以![]() 在区间
在区间![]() 上单调递增,故
上单调递增,故![]() 故
故![]()
所以![]() 在区间
在区间![]() 上单调递增,函数
上单调递增,函数![]()
要使![]() 对于
对于![]() 恒成立,只要
恒成立,只要![]() ,
,
所以![]() 即实数
即实数![]() 的取值范围为
的取值范围为![]() .
.
⑶ 因为![]() 由⑴知,函数
由⑴知,函数![]() 在区间
在区间![]() 上单调递减,在区间
上单调递减,在区间![]() 上单调递增,且
上单调递增,且![]()
不妨设![]() 则
则![]() ,
,
要证![]() 只要证
只要证![]() 即证
即证![]()
因为![]() 在区间
在区间![]() 上单调递增,所以
上单调递增,所以![]()
又![]() 即证
即证![]()
构造函数![]()
即![]()
![]()
因为![]() ,所以
,所以![]() 即
即![]()
所以函数![]() 在区间
在区间![]() 上单调递增,故
上单调递增,故![]()
而![]() 故
故![]()
所以![]() 即
即![]() 所以
所以![]() 成立.
成立.


科目:高中数学 来源: 题型:
【题目】某中学为了解高一年级学生身高发育情况,对全校700名高一年级学生按性别进行分层抽样检查,测得身高(单位: ![]() )频数分布表如表1、表2.
)频数分布表如表1、表2.
表1:男生身高频数分布表
![]()
表2:女生身高频数分布表
![]()
(1)求该校高一女生的人数;
(2)估计该校学生身高在![]() 的概率;
的概率;
(3)以样本频率为概率,现从高一年级的男生和女生中分别选出1人,设![]() 表示身高在
表示身高在![]() 学生的人数,求
学生的人数,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是七位评委为甲,乙两名参赛歌手打出的分数的茎叶图(其中m,n为数字0~9中的一个),则甲歌手得分的众数和乙歌手得分的中位数分别为a和b,则一定有( ) 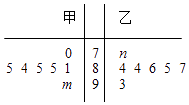
A.a>b
B.a<b
C.a=b
D.a,b的大小与m,n的值有关
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=cos(ωx+ ![]() ),(ω>0,0<φ<π),其中x∈R且图象相邻两对称轴之间的距离为
),(ω>0,0<φ<π),其中x∈R且图象相邻两对称轴之间的距离为 ![]() ;
;
(1)求f(x)的对称轴方程和单调递增区间;
(2)求f(x)的最大值、最小值,并指出f(x)取得最大值、最小值时所对应的x的集合.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,设S为△ABC的面积,满足S= ![]() (a2+b2﹣c2).
(a2+b2﹣c2).
(1)求角C的大小;
(2)求sinA+sinB的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有三个游戏规则如表,袋子中分别装有形状、大小相同的球,从袋中无放回地取球,
游戏1 | 游戏2 | 游戏3 |
袋中装有3个黑球和2个白球 | 袋中装有2个黑球和2个白球 | 袋中装有3个黑球和1个白球 |
从袋中取出2个球 | 从袋中取出2个球 | 从袋中取出2个球 |
若取出的两个球同色,则甲胜 | 若取出的两个球同色,则甲胜 | 若取出的两个球同色,则甲胜 |
若取出的两个球不同色,则乙胜 | 若取出的两个球不同色,则乙胜 | 若取出的两个球不同色,则乙胜 |
问其中不公平的游戏是( )
A.游戏2
B.游戏3
C.游戏1和游戏2
D.游戏1和游戏3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(12分)已知椭圆C:![]() (a>b>0),四点P1(1,1),P2(0,1),P3(–1,
(a>b>0),四点P1(1,1),P2(0,1),P3(–1,![]() ),P4(1,
),P4(1,![]() )中恰有三点在椭圆C上.
)中恰有三点在椭圆C上.
(1)求C的方程;
(2)设直线l不经过P2点且与C相交于A,B两点.若直线P2A与直线P2B的斜率的和为–1,证明:l过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P—ABCD中,平面PAD⊥底面ABCD,其中底面ABCD为等腰梯形,AD∥BC,PA=AB=BC=CD=2,PD=2![]() ,PA⊥PD,Q为PD的中点.
,PA⊥PD,Q为PD的中点.
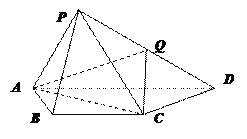
(Ⅰ)证明:CQ∥平面PAB;
(Ⅱ)求直线PD与平面AQC所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】张先生知道清晨从甲地到乙地有好、中、差三个班次的客车.但不知道具体谁先谁后.他打算:第一辆看后一定不坐,若第二辆比第一辆舒服,则乘第二辆;否则坐第三辆.问张先生坐到好车的概率和坐到差车的概率分别是( )
A.![]() 、
、 ![]()
B.![]() 、
、 ![]()
C.![]() 、
、 ![]()
D.![]() 、
、 ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com