练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】有三个游戏规则如表，袋子中分别装有形状、大小相同的球，从袋中无放回地取球，

    游戏1

    游戏2

    游戏3

    袋中装有3个黑球和2个白球

    袋中装有2个黑球和2个白球

    袋中装有3个黑球和1个白球

    从袋中取出2个球

    从袋中取出2个球

    从袋中取出2个球

    若取出的两个球同色，则甲胜

    若取出的两个球同色，则甲胜

    若取出的两个球同色，则甲胜

    若取出的两个球不同色，则乙胜

    若取出的两个球不同色，则乙胜

    若取出的两个球不同色，则乙胜

    问其中不公平的游戏是（ ）
    A.游戏2
    B.游戏3
    C.游戏1和游戏2
    D.游戏1和游戏3

    【答案】C
    【解析】解：对于游戏1，取出两球同色的概率为 ，取出不同色的概率为 ，不公平； 对于游戏2，取出两球同色的概率为 ，取出不同色的概率为 ，不公平；
    对于游戏3，取出两球同色即全是黑球，概率为0.5，取出不同色的也为0.5，公平；
    故选C．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图, 在△中, 点在边上, .

    （Ⅰ）求；

    （Ⅱ）若△的面积是, 求.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥P﹣ABCD中，PA⊥底面ABCD，AB⊥AD，AC⊥CD，∠ABC=60°，PA=AB=BC，E是PC的中点．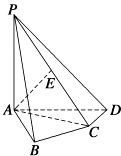
    （1）求PB和平面PAD所成的角的大小；
    （2）证明：AE⊥平面PCD；
    （3）求二面角A﹣PD﹣C得到正弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某公司对新研发的一种产品进行合理定价，且销量与单价具有相关关系，将该产品按事先拟定的价格进行试销，得到如下数据：

    单价x（单位：元）

    8

    8.2

    8.4

    8.6

    8.8

    9

    销量y（单位：万件）

    90

    84

    83

    80

    75

    68


    （1）现有三条y对x的回归直线方程： =﹣10x+170； =﹣20x+250； =﹣15x+210；根据所学的统计学知识，选择一条合理的回归直线，并说明理由．
    （2）预计在今后的销售中，销量与单价服从（1）中选出的回归直线方程，且该产品的成本是每件5元，为使公司获得最大利润，该产品的单价应定多少元？（利润=销售收入﹣成本）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数

    （）当时，求的单调区间和极值.

    （）若对于任意，都有成立，求的取值范围 ；

    （）若且证明：

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】甲、乙两位学生参加数学竞赛培训．现分别从他们在培训期间参加的若干次预赛成绩中随机抽取5次，记录如下：

    甲

    88

    89

    92

    90

    91

    乙

    84

    88

    96

    89

    93

    （Ⅰ）用茎叶图表示这两组数据；
    （Ⅱ）现要从中选派一人参加数学竞赛，你认为选派哪位学生参加合适？请说明理由．（用样本数据特征来说明．）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在物理实验中，为了研究所挂物体的重量x对弹簧长度y的影响．某学生通过实验测量得到物体的重量与弹簧长度的对比表：

    物体重量（单位g）

    1

    2

    3

    4

    5

    弹簧长度（单位cm）

    1.5

    3

    4

    5

    6.5

    参考公式：
    ①．样本数据x1 ， x2 ， …xn的标准差
    s= ，其中 为样本的平均数；
    ②．线性回归方程系数公式 = = ， = ﹣ ．

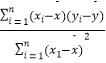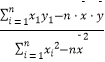    （1）画出散点图；
    （2）利用所给的参考公式，求y对x的回归直线方程；
    （3）预测所挂物体重量为8g时的弹簧长度．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示，已知点A（1，0），D（﹣1，0），点B，C在单位圆O上，且∠BOC= ．
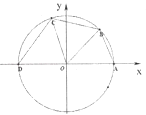
    （Ⅰ）若点B（ ， ），求cos∠AOC的值；
    （Ⅱ）设∠AOB=x（0＜x＜ ），四边形ABCD的周长为y，将y表示成x的函数，并求出y的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=x2+（m+2）x+（2m+5）（m≠0）的两个零点分别在区间（﹣1，0）和区间（1，2）内，则实数m的取值范围是 ．

    查看答案和解析>>

    同步练习册答案