
【题目】如图,在四棱锥P﹣ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点. 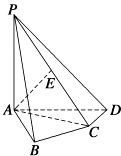
(1)求PB和平面PAD所成的角的大小;
(2)证明:AE⊥平面PCD;
(3)求二面角A﹣PD﹣C得到正弦值.
【答案】
(1)解:在四棱锥P﹣ABCD中,
∵PA⊥底面ABCD,AB平面ABCD,
∴PA⊥AB,又AB⊥AD,PA∩AD=A,
∴AB⊥平面PAD,∴∠APB是PB与平面PAD所成的角,
在Rt△PAB中,AB=PA,∴∠APB=45°,
∴PB和平面PAD所成的角的大小为45°
(2)证明:在四棱锥P﹣ABCD中,
∵PA⊥底面ABCD,CD平面ABCD,∴CD⊥PA,
由条件AC⊥CD,PA⊥底面ABCD,利用三垂线定理得CD⊥PC,PA∩AC=A,
∴CD⊥面PAC,
又AE面PAC,∴AE⊥CD,
由PA=AB=BC,∠ABC=60°,得AC=PA,
∵E是PC的中点,∴AE⊥PC,
又PC∩CD=C,
综上,AE⊥平面PCD.
(3)解:过点E作EM⊥PD,AM在平面PCD内的射影是EM,则AM⊥PD,
∴∠AME是二面角A﹣PD﹣C的平面角,

由已知得∠CAD=30°,
设AC=a,得PA=a,AD= ![]() ,PD=
,PD= ![]() ,AE=
,AE= ![]() ,
,
在Rt△ADP中,∵AM⊥PD,∴AMPD=PAAD,
∴AM= ![]() =
=  ,
,
在Rt△AEM中,sin∠AME= ![]() .
.
∴二面角A﹣PD﹣C得到正弦值为 ![]() .
.
【解析】(1)由线面垂直得PA⊥PB,又AB⊥AD,从而AB⊥平面PAD,进而∠APB是PB与平面PAD所成的角,由此能求出PB和平面PAD所成的角的大小.(2)由线面垂直得CD⊥PA,由条件CD⊥PC,得CD⊥面PAC,由等腰三角形得AE⊥PC,由此能证明AE⊥平面PCD.(3)过点E作EM⊥PD,AM在平面PCD内的射影是EM,则AM⊥PD,由此得∠AME是二面角A﹣PD﹣C的平面角,由此能求出二面角A﹣PD﹣C得到正弦值.


科目:高中数学 来源: 题型:
【题目】小华准备购买一台售价为5000元的电脑,采用分期付款方式,并在一年内将款全部付清,商场提出的 付款方式为:购买后二个月第一次付款,再过二个月第二次付款…,购买后12个月第六次付款,每次付
款金额相同,约定月利率为0.8%每月利息按复利计算.求小华每期付款的金额是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,O是坐标原点,两定点A,B满足| ![]() |=|
|=| ![]() |=
|= ![]()
![]() =2,则点集{P|
=2,则点集{P| ![]() =x
=x ![]() +y
+y ![]() ,|x|+|y|≤1,x,y∈R}所表示的区域的面积是 .
,|x|+|y|≤1,x,y∈R}所表示的区域的面积是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是七位评委为甲,乙两名参赛歌手打出的分数的茎叶图(其中m,n为数字0~9中的一个),则甲歌手得分的众数和乙歌手得分的中位数分别为a和b,则一定有( ) 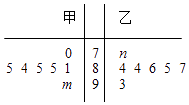
A.a>b
B.a<b
C.a=b
D.a,b的大小与m,n的值有关
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在区间[﹣1,1]上的奇函数,且f(﹣1)=1,若m,n∈[﹣1,1],m+n≠0时,有 ![]() <0.
<0.
(1)解不等式f(x+ ![]() )<f(1﹣x);
)<f(1﹣x);
(2)若f(x)≤t2﹣2at+1对所有x∈[﹣1,1],a∈[﹣1,1]恒成立,求实数t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=cos(ωx+ ![]() ),(ω>0,0<φ<π),其中x∈R且图象相邻两对称轴之间的距离为
),(ω>0,0<φ<π),其中x∈R且图象相邻两对称轴之间的距离为 ![]() ;
;
(1)求f(x)的对称轴方程和单调递增区间;
(2)求f(x)的最大值、最小值,并指出f(x)取得最大值、最小值时所对应的x的集合.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有三个游戏规则如表,袋子中分别装有形状、大小相同的球,从袋中无放回地取球,
游戏1 | 游戏2 | 游戏3 |
袋中装有3个黑球和2个白球 | 袋中装有2个黑球和2个白球 | 袋中装有3个黑球和1个白球 |
从袋中取出2个球 | 从袋中取出2个球 | 从袋中取出2个球 |
若取出的两个球同色,则甲胜 | 若取出的两个球同色,则甲胜 | 若取出的两个球同色,则甲胜 |
若取出的两个球不同色,则乙胜 | 若取出的两个球不同色,则乙胜 | 若取出的两个球不同色,则乙胜 |
问其中不公平的游戏是( )
A.游戏2
B.游戏3
C.游戏1和游戏2
D.游戏1和游戏3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义域为R的奇函数f(x)= ![]() ,其中h(x)是指数函数,且h(2)=4.
,其中h(x)是指数函数,且h(2)=4.
(1)求函数f(x)的解析式;
(2)求不等式f(2x﹣1)>f(x+1)的解集.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com