练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】在△ABC中，角A，B，C所对的边分别为a，b，c，设S为△ABC的面积，满足S= （a2+b2﹣c2）．
    （1）求角C的大小；
    （2）求sinA+sinB的最大值．

    【答案】
    （1）解：由题意可知 absinC= ×2abcosC．

    所以tanC= ．

    因为0＜C＜π，

    所以C=


    （2）解：由已知sinA+sinB

    =sinA+sin（π﹣C﹣A）

    =sinA+sin（ ﹣A）

    =sinA+ cosA+ sinA= sinA+ cosA= sin（A+ ）≤ ．

    当△ABC为正三角形时取等号，

    所以sinA+sinB的最大值是


    【解析】（1）根据三角形的面积公式题中所给条件可得 = absinC，可求出tanC的值，再由三角形内角的范围可求出角C的值．（2）根据三角形内角和为180°将角AB转化为同一个角表示，然后根据两角和的正弦定理可得答案．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】设等差数列{an}满足a3=5，a10=﹣9．
    （1）求{an}的通项公式；
    （2）求{an}的前n项和Sn及使得Sn最大的序号n的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某市居民用水拟实行阶梯水价，每人月用水量中不超过w立方米的部分按4元/立方米收费，超出w立方米的部分按10元/立方米收费，从该市随机调查了10000位居民，获得了他们某月的用水量数据，整理得到如图频率分布直方图：
    （1）如果w为整数，那么根据此次调查，为使80%以上居民在该月的用水价格为4元/立方米，w至少定为多少？
    （2）假设同组中的每个数据用该组区间的右端点值代替，当w=3时，估计该市居民该月的人均水费．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】给出下列命题： ①把函数y=sin（x﹣ ）图象上所有点的横坐标缩短到原来的 倍，纵坐标不变，得到函数y=sin（2x﹣ ）；
    ②若α，β是第一象限角且α＜β，则cosα＞cosβ；
    ③x=﹣ 是函数y=cos（2x+ π）的一条对称轴；
    ④函数y=4sin（2x+ ）与函数y=4cos（2x﹣ ）相同；
    ⑤y=2sin（2x﹣ ）在[0， ]是增函数；
    则正确命题的序号 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】直线y=x+b与曲线x= 恰有一个公共点，则b的取值范围是 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数

    （）当时，求的单调区间和极值.

    （）若对于任意，都有成立，求的取值范围 ；

    （）若且证明：

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在任意三角形ABC内任取一点Q，使S△ABQ≥ S△ABC的概率为 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某校在一次趣味运动会的颁奖仪式上，高一、高二、高三各代表队人数分别为120人、120人、n人．为了活跃气氛，大会组委会在颁奖过程中穿插抽奖活动，并用分层抽样的方法从三个代表队中共抽取20人在前排就坐，其中高二代表队有6人．
    （1）求n的值；
    （2）把在前排就坐的高二代表队6人分别记为a，b，c，d，e，f，现随机从中抽取2人上台抽奖．求a和b至少有一人上台抽奖的概率．
    （3）抽奖活动的规则是：代表通过操作按键使电脑自动产生两个[0，1]之间的均匀随机数x，y，并按如图所示的程序框图执行．若电脑显示“中奖”，则该代表中奖；若电脑显示“谢谢”，则不中奖，求该代表中奖的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

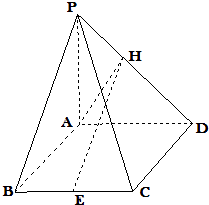
    【题目】如图，已知四棱锥P﹣ABCD中，底面ABCD是棱长为2的菱形，PA⊥平面ABCD，∠ABC=60°，E是BC中点，若H为PD上的动点，EH与平面PAD所成最大角的正切值为 ．
    （1）当EH与平面PAD所成角的正切值为 时，求证：EH∥平面PAB；
    （2）在（1）的条件下，求二面角A﹣PB﹣C的余弦值．

    查看答案和解析>>

    同步练习册答案