练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    8．已知△ABC的三个内角A，B，C所对的边分别是a，b，c，且3bcosA-3acosB=c，则下列结论正确的是（　　）
    A．tanB•tanA=2BB．tanA=2tanBC．tanB=2tanAD．tanA+tanB=2

    分析 由题意和正弦定理可得3sinBcosA-3sinAcosB=sinC=sin（A+B），由三角函数的和差角公式及弦化切的思想可得结论．

    解答 解：∵△ABC的三个角A，B，C所对的边分别是a，b，c，且3bcosA-3acosB=c，
    由正弦定理可得3sinBcosA-3sinAcosB=sinC，
    ∴3sinBcosA-3sinAcosB=sin（A+B），
    ∴3sinBcosA-3sinAcosB=sinBcosA+sinAcosB，
    即2sinBcosA=4sinAcosB，
    两边同除以cosAcosB，
    得2tanB=4tanA，
    即tanB=2tanA．
    故选：C．

    点评 本题考查了正弦定理以及三角函数公式和弦化切的思想应用问题，属基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    18．若a=20.5，b=logπ3，c=log20.9，则（　　）
    A．a＞b＞cB．b＞a＞cC．c＞a＞bD．b＞c＞a

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    19．某公司的广告费支出x与销售额y（单位：万元）之间有下列对应数据：
    x24568
    y40605070
    已知y对x呈线性相关关系，且回归方程为$\stackrel{∧}{y}$═6.5x+17.5，工作人员不慎将表格中y的第一个数据遗失，该数据为30．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    16．如图，在四棱锥O-ABCD中，底面ABCD是边长为1的菱形，∠ABC=$\frac{π}{4}$，OA⊥底面ABCD，OA=2，M为OA的中点，N为BC的中点．
    （1）证明：直线MN∥平面OCD．
    （2）求三棱锥N-CDM的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．边长为1，$\sqrt{5}$，$2\sqrt{2}$的三角形，它的最大角与最小角的和是（　　）
    A．60°B．120°C．135°D．150°

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

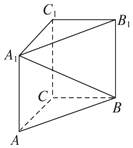    13．如图，在直三棱柱ABC-A1B1C1中，∠ACB=90°，AA1=2，AC=BC=1，则异面直线A1B与AC所成角的余弦值是（　　）
    A．$\frac{{\sqrt{6}}}{5}$B．$\frac{{\sqrt{6}}}{4}$C．$\frac{{\sqrt{6}}}{3}$D．$\frac{{\sqrt{6}}}{6}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（{a＞b＞0}）$的一条渐近线平行于直线l：y=-2x-10，双曲线的一个焦点在直线l上，双曲线的方程为（　　）
    A．$\frac{x^2}{20}-\frac{y^2}{5}=1$B．$\frac{x^2}{20}-\frac{y^2}{100}=1$C．$\frac{x^2}{5}-\frac{y^2}{20}=1$D．$\frac{x^2}{25}-\frac{y^2}{100}=1$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    17．设P为直线x-y=0上的一动点，过P点做圆（x-4）2+y2=2的两条切线，切点分别为A，B，则∠APB的最大值60°．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    8．为了调查患慢性气管炎是否与吸烟有关，调查了100名50岁以下的人，调查结果如下表：
    患慢性气管炎未患慢性气管炎合计
    吸烟202040
    不吸烟55560
    合计2575100
    根据列联表数据，有99.9%的把握（填写相应的百分比）认为患慢性气管炎与吸烟有关．
    附：
    P（K2≥k）  0.0500.0100.001
    k   3.8416.63510.828
    ${K^2}=\frac{{n{{（ad-bc）}^2}}}{（a+b）（c+d）（a+c）（b+d）}$．

    查看答案和解析>>

    同步练习册答案