
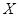 表示所取3张卡片上的数字的中位数,求
表示所取3张卡片上的数字的中位数,求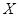 的分布列与数学期望.
的分布列与数学期望.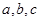 满足
满足 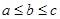 ,则称
,则称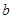 为这三个数的中位数).
为这三个数的中位数). 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:不详 题型:解答题
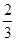 和
和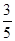 ,现安排甲组研发新产品
,现安排甲组研发新产品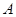 ,乙组研发新产品
,乙组研发新产品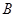 .设甲,乙两组的研发是相互独立的.
.设甲,乙两组的研发是相互独立的.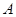 研发成功,预计企业可获得
研发成功,预计企业可获得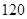 万元,若新产品
万元,若新产品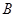 研发成功,预计企业可获得利润
研发成功,预计企业可获得利润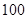 万元,求该企业可获得利润的分布列和数学期望.
万元,求该企业可获得利润的分布列和数学期望.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
A.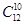 ( (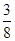 )10( )10(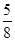 )2 )2 | B.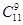 ( (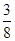 )9( )9(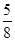 )2× )2×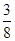 |
C.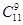 ( (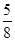 )9( )9(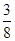 )2 )2 | D.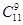 ( (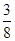 )9( )9(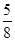 )2 )2 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.3 | B.4 | C.2和5 | D.3和4 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| ξ | 0 | 2 | 3 | 4 | 5 |
| P | 0.03 | P1 | P2 | P3 | P4 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com