
| A.3 | B.4 | C.2和5 | D.3和4 |
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
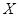 表示所取3张卡片上的数字的中位数,求
表示所取3张卡片上的数字的中位数,求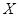 的分布列与数学期望.
的分布列与数学期望.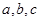 满足
满足 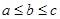 ,则称
,则称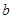 为这三个数的中位数).
为这三个数的中位数).查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
A.(0,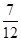 ) ) | B.(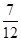 ,1) ,1) | C.(0,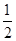 ) ) | D.(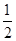 ,1) ,1) |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
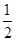 .
.
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| | 文艺节目 | 新闻节目 | 总计 |
| 20至40岁 | 40 | 18 | 58 |
| 大于40岁 | 15 | 27 | 42 |
| 总计 | 55 | 45 | 100 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.88% | B.90% | C.92% | D.94% |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
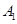 ,
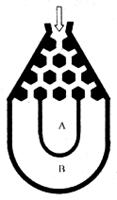
, (如图)这8个点中任取两点分别分终点得到两个向量,记这两个向量的数量积为X。若X=0就参加学校合唱团,否则就参加学校排球队。
(如图)这8个点中任取两点分别分终点得到两个向量,记这两个向量的数量积为X。若X=0就参加学校合唱团,否则就参加学校排球队。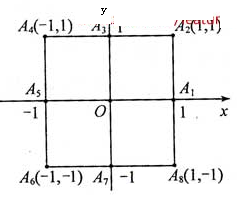
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com