
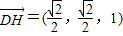 .
.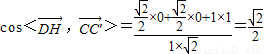 ,求出
,求出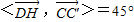 .即可.
.即可.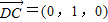 .通过
.通过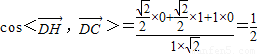 ,得到
,得到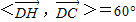 .即可.
.即可.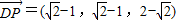 解题过程同方法一.
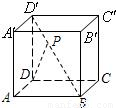
解题过程同方法一.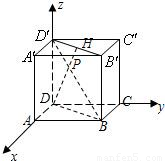 解:方法一:如图,以D为原点,DA为单位长建立空间直角坐标系D-xyz.
解:方法一:如图,以D为原点,DA为单位长建立空间直角坐标系D-xyz.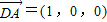 ,
,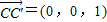 .连接BD,B'D'.
.连接BD,B'D'.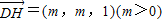 ,由已知
,由已知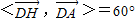 ,
,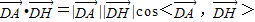
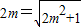 .解得
.解得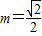 ,所以
,所以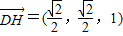 .(4分)
.(4分)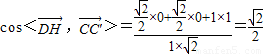 ,
,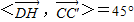 .即DP与CC'所成的角为45°.(8分)
.即DP与CC'所成的角为45°.(8分)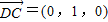 .
.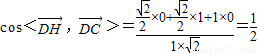 ,所以
,所以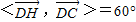 .
.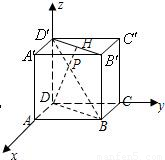 方法二:如图,以D为原点,DA为单位长建立空间直角坐标
方法二:如图,以D为原点,DA为单位长建立空间直角坐标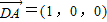 ,
,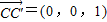 ,
,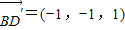 .
.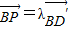 ,∴(x-1,y-1,z)=(-λ,-λ,λ)
,∴(x-1,y-1,z)=(-λ,-λ,λ)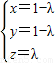 ,则
,则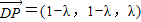 ,由已知,
,由已知,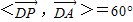 ,
,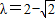 ,∴
,∴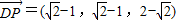 (4分)
(4分)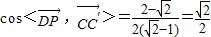 ,
,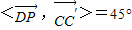 .即DP与CC'所成的角为45°.(8分)
.即DP与CC'所成的角为45°.(8分)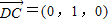 .
.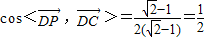 ,所以
,所以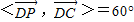 .
.

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:044
如图,已知过原点O从x轴正方向出发顺时针转60°得到射线t,点A(x,y)在射线t上![]() x>0,y<0
x>0,y<0![]() ,设|OA|=m;又点B(
,设|OA|=m;又点B(![]() ,
,![]() )在射线y=0(
)在射线y=0(![]() >0)上移动;设点P为第四象限的动点,若
>0)上移动;设点P为第四象限的动点,若![]() ·
·![]() =0,且
=0,且![]() ·
·![]() ,
,![]()
![]() ·
·![]() ,
,![]() 成等差数列.
成等差数列.
(Ⅰ)求动点P的轨迹方程,并说明轨迹C的形状;
(Ⅱ)已知动直线l与曲线C有三个不同的交点M、N,且![]() ∥v,v=(2,1),设 Q(
∥v,v=(2,1),设 Q(![]() ,
,![]() )为线段MN的中点,求
)为线段MN的中点,求![]() 的取值范围.
的取值范围.

查看答案和解析>>
科目:高中数学 来源:数学教研室 题型:044
(Ⅰ)求动点P的轨迹方程,并说明轨迹C的形状;
(Ⅱ)已知动直线l与曲线C有三个不同的交点M、N,且![]() ∥v,v=(2,1),设 Q(
∥v,v=(2,1),设 Q(![]() ,
,![]() )为线段MN的中点,求
)为线段MN的中点,求![]() 的取值范围.
的取值范围.

查看答案和解析>>
科目:高中数学 来源:同步题 题型:解答题
 的概率P1;
的概率P1; 的概率P2。
的概率P2。
查看答案和解析>>
科目:高中数学 来源: 题型:
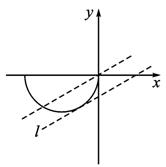
(1)试问点P的轨迹是什么曲线?
(2)已知直线l的斜率为![]() ,若直线l与曲线C有两个不同的交点M,N,设线段MN的中点为Q,求点Q的横坐标的取值范围.
,若直线l与曲线C有两个不同的交点M,N,设线段MN的中点为Q,求点Q的横坐标的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com