已知函数f(x)=lnx+a(x2-x)
(1)当a=-1时,求函数f(x)的单调区间和极值;
(2)若f(x)存在单调递减区间,求实数a的取值范围.
(3)比较lnn与n2-n(n∈N*)的大小,并证明你的结论.
解:(1)当a=-1,f(x)=lnx-x
2+x,x>0,
f′(x)=

-2x+1,
令f′(x)=0,得

-2x+1=0,
∴2x
2-x-1=0,
(2x+1)(x-1)=0,
x=1或x=-

(舍),
列表讨论:
| x | (0,1) | 1 | (1,+∞) |
| f′(x) | + | 0 | - |
| f(x) | ↑ | 极大值 | ↓ |
∴函数f(x)的单调增区间是(0,1);函数f(x)的单调减区间是(1,+∞).
函数不存在极小值,当x=1时取得极大值,
极大值为f(1)=ln1-1+1=0.
(2)∵f(x)=lnx+a(x
2-x)的定义域为(0,+∞),且f(x)存在单调递减区间,
∴
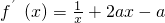
=
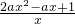
≤0在(0,+∞)有解,
即2ax
2-ax+1≤0在(0,+∞)有解,
∴

,
解得a≥8,或a<0.
故实数a的取值范围{a|a≥8,或a<0}.
(3)lnn≤n
2-n,(n∈N
*).
证明:由(1)知,n∈N
*时,f(n)=lnn-n
2+n是减函数,
且最大值为f(1)=ln1-1+1=0,
∴f(n)=lnn-n
2+n≤0,
∴lnn≤n
2-n,(n∈N
*).
分析:(1)当a=-1,f(x)=lnx-x
2+x,x>0,故f′(x)=

-2x+1,令f′(x)=0,得x=1或x=-

(舍),列表讨论,能求出函数f(x)的单调区间和极值.
(2)由f(x)=lnx+a(x
2-x)的定义域为(0,+∞),且f(x)存在单调递减区间,知
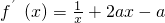
=
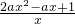
≤0在(0,+∞)有解,即2ax
2-ax+1≤0在(0,+∞)有解,由此能求出实数a的取值范围.
(3)由(1)知,n∈N
*时,f(n)=lnn-n
2+n是减函数,且最大值为f(1)=ln1-1+1=0,故f(n)=lnn-n
2+n≤0,由此能比较lnn与n
2-n,(n∈N
*)的大小.
点评:本题考查函数的单调区间、极值的求法,判断实数的取值范围,比较大小.综合性强,难度大.解题时要认真审题,仔细解答,注意合理地进行等价转化.

 -2x+1,
-2x+1, -2x+1=0,
-2x+1=0, (舍),
(舍),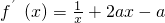 =
=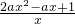 ≤0在(0,+∞)有解,
≤0在(0,+∞)有解, ,
, -2x+1,令f′(x)=0,得x=1或x=-
-2x+1,令f′(x)=0,得x=1或x=- (舍),列表讨论,能求出函数f(x)的单调区间和极值.
(舍),列表讨论,能求出函数f(x)的单调区间和极值.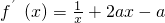 =
=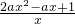 ≤0在(0,+∞)有解,即2ax2-ax+1≤0在(0,+∞)有解,由此能求出实数a的取值范围.
≤0在(0,+∞)有解,即2ax2-ax+1≤0在(0,+∞)有解,由此能求出实数a的取值范围.
