
【题目】已知函数![]() ,
,![]() ,其中
,其中![]() 为自然对数的底数,
为自然对数的底数,![]() .
.
(1)求证:![]() ;
;
(2)若对于任意![]() ,
,![]() 恒成立,求
恒成立,求![]() 的取值范围;
的取值范围;
(3)若存在![]() ,使
,使![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)证明见解析;
(2)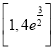 ;
;
(3)![]() 或
或![]() .
.
【解析】
(1)对利用导数研究函数的单调性及最小值,进而证明不等式;
(2)由题意得![]() ,对
,对![]() 分成
分成![]() 三种情况讨论,进而利用参变分离,构造新函数,利用导数研究新函数的最值,从而得到
三种情况讨论,进而利用参变分离,构造新函数,利用导数研究新函数的最值,从而得到![]() 的取值范围;
的取值范围;
(3)设![]() ,题设等价于函数
,题设等价于函数![]() 有零点时的
有零点时的![]() 的取值范围,先对函数进行求导得
的取值范围,先对函数进行求导得![]() ,再对
,再对![]() 分成
分成![]() 三种情况进行研究函数的零点.
三种情况进行研究函数的零点.
解:(1)令![]() ,得
,得![]() ,
,
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,
,
所以函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
所以函数![]() 在
在![]() 处取得最小值,因为
处取得最小值,因为![]() ,
,
所以![]() .
.
(2)由题意,得![]() ,
,
当![]() ,不等式显然成立,此时
,不等式显然成立,此时![]() ;
;
当![]() 时,
时,![]() ,所以
,所以![]() ,
,
当![]() 时,
时,![]() ,所以
,所以![]() ,
,
记![]() ,
,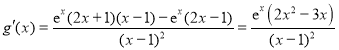 ,
,
∴![]() 在区间
在区间![]() 和
和![]() 上为增函数,
上为增函数,![]() 和
和![]() 上为减函数.
上为减函数.
∴当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,
,
综上所述![]() 的取值范围为
的取值范围为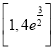 .
.
(3)设![]() ,题设等价于函数
,题设等价于函数![]() 有零点时的
有零点时的![]() 的取值范围.
的取值范围.
![]()
当![]() ,
,![]() ,
,![]() 恒成立,
恒成立,
所以![]() 在
在![]() 单调递增,
单调递增,
![]() ,
,
若![]() ,则
,则![]() ,
,
只需![]() ,则
,则![]() ,则
,则![]() ,
,
所以![]() 有零点.
有零点.
当![]() 时,
时,![]() ,对
,对![]() 恒成立,
恒成立,
所以![]() 无零点,不成立.
无零点,不成立.
当![]() 时,
时,![]() ,得
,得![]() ,
,
则![]() 时
时![]() ,所以
,所以![]() 在
在![]() 单调递减;
单调递减;
![]() 时
时![]() ,所以
,所以![]() 在在
在在![]() 单调递增,
单调递增,
所以![]() ,
,
①![]() 时,
时,![]() ,
,![]() ,
,
又![]() ,
,
所以![]() 有零点;
有零点;
②![]() 时,
时,![]() ,
,![]()
所以![]() 有零点;
有零点;
③![]() 时,
时,![]() ,
,![]() ,
,
所以![]() 无零点,不成立.
无零点,不成立.
综上,![]() 的取值范围是
的取值范围是![]() 或
或![]() .
.


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的一个焦点与抛物线
的一个焦点与抛物线![]() 的焦点重合,且此抛物线的准线被椭圆
的焦点重合,且此抛物线的准线被椭圆![]() 截得的弦长为
截得的弦长为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)直线![]() 交椭圆
交椭圆![]() 于
于![]() 、
、![]() 两点,线段
两点,线段![]() 的中点为
的中点为![]() ,直线
,直线![]() 是线段
是线段![]() 的垂直平分线,试问直线
的垂直平分线,试问直线![]() 是否过定点?若是,请求出该定点的坐标;若不是,请说明理由.
是否过定点?若是,请求出该定点的坐标;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂生产一批零件,为了解这批零件的质量状况,检验员从这批产品中随机抽取了100件作为样本进行检测,将它们的重量(单位:g)作为质量指标值,由检测结果得到如下频率分布表和频率分布直方图.
分组 | 频数 | 频率 |
| 8 | |
| ||
| ||
| 16 | 0.16 |
| 4 | 0.04 |
合计 | 100 | 1 |
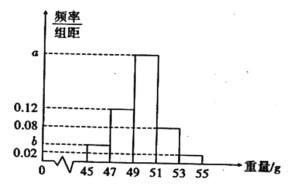
(1)求图中![]() ,
,![]() 的值;
的值;
(2)根据质量标准规定:零件重量小于47或大于53为不合格品,重量在区间![]() 和
和![]() 内为合格品,重量在区间
内为合格品,重量在区间![]() 内为优质品.已知每件产品的检测费用为5元,每件不合格品的回收处理费用为20元.以抽检样本重量的频率分布作为该批零件重量的概率分布.若这批零件共400件,现有两种销售方案:
内为优质品.已知每件产品的检测费用为5元,每件不合格品的回收处理费用为20元.以抽检样本重量的频率分布作为该批零件重量的概率分布.若这批零件共400件,现有两种销售方案:
方案一:对剩余零件不再进行检测,回收处理这100件样本中的不合格品,余下所有零件均按150元/件售出;
方案二:继续对剩余零件的重量进行逐一检测,回收处理所有不合格品,合格品按150元/件售出,优质品按200元/件售出.
仅从获得利润大的角度考虑,该生产商应选择哪种方案?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某项娱乐活动的海选过程中评分人员需对同批次的选手进行考核并评分,并将其得分作为该选手的成绩,成绩大于等于60分的选手定为合格选手,直接参加第二轮比赛,不超过40分的选手将直接被淘汰,成绩在![]() 内的选手可以参加复活赛,如果通过,也可以参加第二轮比赛.
内的选手可以参加复活赛,如果通过,也可以参加第二轮比赛.
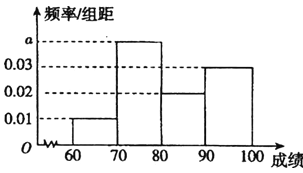
(1)已知成绩合格的200名参赛选手成绩的频率分布直方图如图,求a的值及估计这200名参赛选手的成绩平均数;
(2)根据已有的经验,参加复活赛的选手能够进入第二轮比赛的概率为![]() ,假设每名选手能否通过复活赛相互独立,现有3名选手进入复活赛,记这3名选手在复活赛中通过的人数为随机变量X,求X的分布列和数学期望.
,假设每名选手能否通过复活赛相互独立,现有3名选手进入复活赛,记这3名选手在复活赛中通过的人数为随机变量X,求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某研究机构为了解某学校学生使用手机的情况,在该校随机抽取了60名学生(其中男、女生人数之比为2:1)进行问卷调查.进行统计后将这60名学生按男、女分为两组,再将每组学生每天使用手机的时间(单位:分钟)分为![]() 5组,得到如图所示的频率分布直方图(所抽取的学生每天使用手机的时间均不超过50分钟).
5组,得到如图所示的频率分布直方图(所抽取的学生每天使用手机的时间均不超过50分钟).
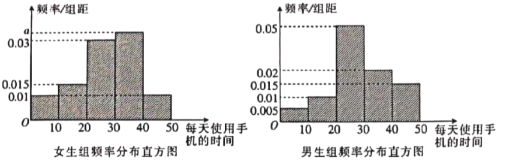
(1)求出女生组频率分布直方图中![]() 的值;
的值;
(2)求抽取的60名学生中每天使用手机时间不少于30分钟的学生人数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代的数学名著,书中有如下问题:“今有五人分五钱,令上二人所得与下三人等.问各得几何.”其意思为“已知甲、乙、丙、丁、戊五人分5钱,甲、乙两人所得与丙、丁、戊三人所得相同,且甲、乙、丙、丁、戊所得依次成等差数列.问五人各得多少钱?”(“钱”是古代的一种重量单位).这个问题中,丙所得为( )
A.![]() 钱B.1钱C.
钱B.1钱C.![]() 钱D.
钱D.![]() 钱
钱
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列![]() ,
,![]() 及函数
及函数![]() (
(![]() ),
),![]() (
(![]() ).
).
(1)若等比数列![]() 满足
满足![]() ,
,![]() ,
,![]() ,求数列
,求数列![]() 的前
的前![]() (
(![]() )项和;
)项和;
(2)已知等差数列![]() 满足
满足![]() ,
,![]() ,
,![]() (
(![]() 、
、![]() 均为常数,
均为常数,![]() ,且
,且![]() ),
),![]() (
(![]() ).试求实数对(
).试求实数对(![]() ,
,![]() ),使得
),使得![]() 成等比数列.
成等比数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有人玩掷均匀硬币走跳棋的游戏,棋盘上标有第0站(出发地),第1站,第2站,……,第100站. 一枚棋子开始在出发地,棋手每掷一次硬币,这枚棋子向前跳动一次,若掷出正向,棋子向前跳一站,若掷出反面,棋子向前跳两站,直到棋子跳到第99站(获胜)或跳到第100站(失败)时,该游戏结束. 设棋子跳到第![]() 站的概率为
站的概率为![]() .
.
(1)求![]() ,
,![]() ,
,![]() ,并根据棋子跳到第
,并根据棋子跳到第![]() 站的情况写出
站的情况写出![]() 与
与![]() 、
、![]() 的递推关系式(
的递推关系式(![]() );
);
(2)求证:数列![]()
![]() 为等比数列;
为等比数列;
(3)求玩该游戏获胜的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com