(理科)已知函数y=f(x),x∈R满足f(x+1)=af(x),a是不为0的实常数.
(1)若函数y=f(x),x∈R是周期函数,写出符合条件a的值;
(2)若当0≤x<1时,f(x)=x(1-x),且函数y=f(x)在区间[0,+∞)上的值域是闭区间,求a的取值范围;
(3)若当0<x≤1时,f(x)=3x+3-x,试研究函数y=f(x)在区间(0,+∞)上是否可能是单调函数?若可能,求出a的取值范围;若不可能,请说明理由.
解:(1)a=1时,T=1,
a=-1时,f(x+1)=-f(x),f(x+2)=-f(x+1)=f(x),
∴T=2;
(2)当n≤x≤n+1(n≥0,n∈Z)时,f
n(x)=af
n-1(x-1)=a
2f
n-1(x-2)=…=a
nf
1(x-n),∴f
n(x)=a
n(x-n)(n+1-x),
∴
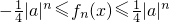
;
当|a|>1时f(x)∈(-∞,+∞)舍去;
当a=1时
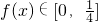
符合,当a=-1时
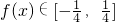
符合;
当0<a<1时
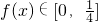
符合,当-1<a<0时
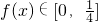
符合;∴a∈[-1,0)∪(0,1].
(3)当n≤x≤n+1(n≥0,n∈Z)时,f
n(x)=af
n-1(x-1)=a
2f
n-1(x-2)=…=a
nf
1(x-n),∴f
n(x)=a
n(3
x-n+3
n-x);
易证函数f
n(x)=a
n(3
x-n+3
n-x),x∈[n,n+1],n≥0,n∈Z当a>0时是增函数,
此时∴
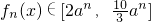
,
若函数y=f(x)在区间[0,+∞)上是单调增函数,则必有
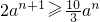
,解得:

;
显然当a<0时,函数y=f(x)在区间[0,+∞)上不是单调函数;
所以

.
分析:(1)先求出当a=1时,得到T=1,再求当a=-1时,f(x+1)=-f(x),f(x+2)=-f(x+1)=f(x),然后再求周期.
(2)在区间[n,n+1)上取变量,利用“f(x+1)=af(x)”逐步将变量转化到区间[0,1]上,用f(x)=x(1-x)求解.
(3)由于f
n(x)=a
n(3
x-n+3
n-x),易知f
n(x)=a
n(3
x-n+3
n-x),x∈[n,n+1],n≥0,n∈Z当a>0时是增函数,由“函数y=f(x)在区间[0,+∞)上是单调增函数”,有
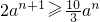
求解即可.
点评:本小题主要考查函数单调性的应用、函数的周期性、函数与方程的综合运用等基础知识,考查运算求解能力,考查化归与转化思想.属于基础题.

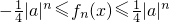 ;
;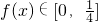 符合,当a=-1时
符合,当a=-1时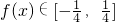 符合;
符合;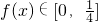 符合,当-1<a<0时
符合,当-1<a<0时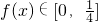 符合;∴a∈[-1,0)∪(0,1].
符合;∴a∈[-1,0)∪(0,1].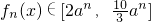 ,
,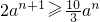 ,解得:
,解得: ;
; .
.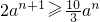 求解即可.
求解即可.

 一本好题口算题卡系列答案
一本好题口算题卡系列答案