
【题目】设对于任意实数x,不等式|x+6|+|x﹣1|≥m恒成立. (I) 求m 的取值范围;
(Ⅱ)当m取最大值时,解关于x的不等式:|x﹣4|﹣3x≤2m﹣9.
【答案】解:(I)∵|x+6|+|x﹣1|≥|x+6﹣x+1|=7, 又对于任意实数x,不等式|x+6|+|x﹣1|≥m恒成立,
∴m≤7,
∴m 的取值范围是(﹣∞,7].
(Ⅱ)当m取最大值时,m=7,
原不等式等价于:|x﹣4|﹣3x≤5,
∴ ![]() 或
或 ![]() ,
,
解得x≥4或﹣ ![]() ≤x<4,
≤x<4,
∴原不等式的解集为{x|x≥﹣ ![]() }
}
【解析】(1)由|x+6|+|x﹣1|≥|x+6﹣x+1|=7,能求出m 的取值范围.(2)当m取最大值时,m=7,原不等式等价于:|x﹣4|﹣3x≤5,由此能求出原不等式的解集.
【考点精析】关于本题考查的绝对值不等式的解法,需要了解含绝对值不等式的解法:定义法、平方法、同解变形法,其同解定理有;规律:关键是去掉绝对值的符号才能得出正确答案.


 考前必练系列答案
考前必练系列答案科目:高中数学 来源: 题型:
【题目】在△ABC中,已知C= ![]() ,向量
,向量 ![]() =(sinA,1),
=(sinA,1), ![]() =(1,cosB),且
=(1,cosB),且 ![]() .
.
(1)求A的值;
(2)若点D在边BC上,且3 ![]() =
= ![]() ,
, ![]() =
= ![]() ,求△ABC的面积.
,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
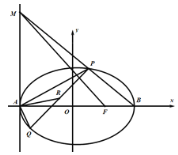
【题目】在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() 的左右顶点为
的左右顶点为![]() ,右焦点为
,右焦点为![]() ,一条准线方程是
,一条准线方程是![]() ,点
,点![]() 为椭圆
为椭圆![]() 上异于
上异于![]() 的两点,点
的两点,点![]() 为
为![]() 的中点.
的中点.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)直线![]() 交直线
交直线![]() 于点
于点![]() ,记直线
,记直线![]() 的斜率为
的斜率为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,求证:
,求证:![]() 为定值;
为定值;
(3)若![]() ,求直线
,求直线![]() 斜率的取值范围。
斜率的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代数学著作《九章算术》有如下问题:“今有人持金出五关,前关二而税一,次关三而税一,次关四而税一,次关五而税一,次关六而税一,并五关所税,适重一斤,问本持金几何”其意思为“今有人持金出五关,第1关收税金 ![]() ,第2关收税金为剩余金的
,第2关收税金为剩余金的 ![]() ,第3关收税金为剩余金的
,第3关收税金为剩余金的 ![]() ,第4关收税金为剩余金的
,第4关收税金为剩余金的 ![]() ,第5关收税金为剩余金的
,第5关收税金为剩余金的 ![]() ,5关所收税金之和,恰好重1斤,问原来持金多少?”若将题中“5关所收税金之和,恰好重1斤,问原来持金多少?”改成假设这个原来持金为x,按此规律通过第8关,则第8关需收税金为x.
,5关所收税金之和,恰好重1斤,问原来持金多少?”若将题中“5关所收税金之和,恰好重1斤,问原来持金多少?”改成假设这个原来持金为x,按此规律通过第8关,则第8关需收税金为x.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点A(0,-2),椭圆E: ![]() (a>b>0)的离心率为
(a>b>0)的离心率为![]() ,F是椭圆E的右焦点,直线AF的斜率为
,F是椭圆E的右焦点,直线AF的斜率为![]() ,O为坐标原点.
,O为坐标原点.
(1)求E的方程;
(2)设过点A的动直线l与E相交于P,Q两点.当△OPQ的面积最大时,求l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆:![]() 的四个顶点围成的四边形的面积为
的四个顶点围成的四边形的面积为![]() ,原点到直线
,原点到直线![]() 的距离为
的距离为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)已知定点![]() ,是否存在过
,是否存在过![]() 的直线
的直线![]() ,使
,使![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,且以
两点,且以![]() 为直径的圆过椭圆
为直径的圆过椭圆![]() 的左顶点?若存在,求出
的左顶点?若存在,求出![]() 的方程:若不存在,请说明理由.
的方程:若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在几何体A1B1D1﹣ABCD中,四边形A1B1BA与A1D1DA均为直角梯形,且AA1⊥底面ABCD,四边形ABCD为正方形,AB=2A1D1=2A1B1=4,AA1=4,P为DD1的中点. 
(Ⅰ)求证:AB1⊥PC;
(Ⅱ)求几何体A1B1D1﹣ABCD的表面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)= ![]() ,若曲线f(x)在点(e,f(e))处的切线与直线e2x﹣y+e=0垂直(其中e为自然对数的底数).
,若曲线f(x)在点(e,f(e))处的切线与直线e2x﹣y+e=0垂直(其中e为自然对数的底数).
(1)若f(x)在(m,m+1)上存在极值,求实数m的取值范围;
(2)求证:当x>1时, ![]() >
> ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题![]() 关于
关于![]() 的不等式
的不等式![]() 的解集是
的解集是![]() ,命题
,命题![]() 函数
函数![]() 的定义域为
的定义域为![]() .
.
(1)如果![]() 为真命题,求实数
为真命题,求实数![]() 的取值范围;
的取值范围;
(2)如果![]() 为真命题,
为真命题, ![]() 为假命题, 求实数
为假命题, 求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com