
【题目】如图,三棱柱![]() 中,
中,![]() ,
,![]() ,平面
,平面![]() 平面
平面![]() .
.
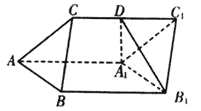
(1)求证:![]() ;
;
(2)若![]() ,直线
,直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,
,![]() 为
为![]() 的中点,求二面角
的中点,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析(2)![]()
【解析】
(1)过点C作CO⊥AA1,则CO⊥平面AA1B1B,CO⊥OB,推导出Rt△AOC≌Rt△BOC,从而AA1⊥OB,再由AA1⊥CO,得AA1⊥平面BOC,由此能证明AA1⊥BC.
(2)以O为坐标原点,OA,OB,OC所在直线分别为x,y,z轴,建立空间直角坐标系,利用向量法能求出二面角B1﹣A1D﹣C1的余弦值.
(1)过点![]() 作
作![]() ,垂足为
,垂足为![]() ,
,
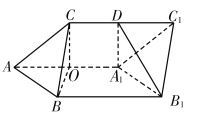
因为平面![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,故
,故![]() ,
,
又因为![]() ,
,![]() ,
,![]() ,
,
所以![]() ,故
,故![]() ,
,
因为![]() ,所以
,所以![]() ,
,
又因为![]() ,所以
,所以![]() 平面
平面![]() ,故
,故![]() .
.
(2)以![]() 为坐标原点,
为坐标原点,![]() ,
,![]() ,
,![]() 所在直线为
所在直线为![]() ,
,![]() ,
,![]() 轴,建立空间直角坐标系
轴,建立空间直角坐标系![]() ,
,
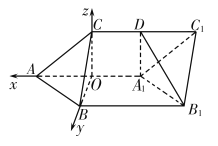
因为![]() 平面
平面![]() ,
,
所以![]() 是直线
是直线![]() 与平面
与平面![]() 所成角,
所成角,
故![]() ,
,
所以![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,则
,则
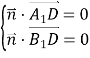 ,所以
,所以![]() ,
,
令![]() ,得
,得![]() ,
,
因为![]() 平面
平面![]() ,
,
所以![]() 为平面
为平面![]() 的一条法向量,
的一条法向量,
![]() ,
,
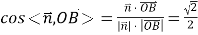 ,
,
所以二面角![]() 的余弦值为
的余弦值为![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】2018年辽宁省正式实施高考改革.新高考模式下,学生将根据自己的兴趣、爱好、学科特长和高校提供的“选考科目要求”进行选课.这样学生既能尊重自己爱好、特长做好生涯规划,又能发挥学科优势,进而在高考中获得更好的成绩和实现自己的理想.考改实施后,学生将在高二年级将面临着![]() 的选课模式,其中“3”是指语、数、外三科必学内容,“1”是指在物理和历史中选择一科学习,“2”是指在化学、生物、地理、政治四科中任选两科学习.某校为了更好的了解学生对“1”的选课情况,学校抽取了部分学生对选课意愿进行调查,依据调查结果制作出如下两个等高堆积条形图:根据这两幅图中的信息,下列哪个统计结论是不正确的( )
的选课模式,其中“3”是指语、数、外三科必学内容,“1”是指在物理和历史中选择一科学习,“2”是指在化学、生物、地理、政治四科中任选两科学习.某校为了更好的了解学生对“1”的选课情况,学校抽取了部分学生对选课意愿进行调查,依据调查结果制作出如下两个等高堆积条形图:根据这两幅图中的信息,下列哪个统计结论是不正确的( )
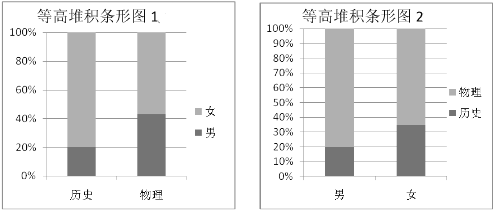
A.样本中的女生数量多于男生数量
B.样本中有学物理意愿的学生数量多于有学历史意愿的学生数量
C.样本中的男生偏爱物理
D.样本中的女生偏爱历史
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() ,曲线
,曲线![]() ,且
,且![]() 与
与![]() 的焦点之间的距离为
的焦点之间的距离为![]() ,且
,且![]() 与
与![]() 在第一象限的交点为
在第一象限的交点为![]() .
.
(1)求曲线![]() 的方程和点
的方程和点![]() 的坐标;
的坐标;
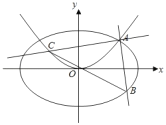
(2)若过点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 与
与![]() 的另一个交点为
的另一个交点为![]() ,过点
,过点![]() 与
与![]() 垂直的直线与
垂直的直线与![]() 的另一个交点为
的另一个交点为![]() .设
.设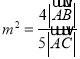 ,试求
,试求![]() 取值范围.
取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随机抽取某中学甲、乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图所示.
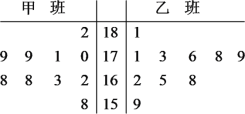
(1)试比较甲、乙两班分别抽取的这10名同学身高的中位数大小;
(2)现从乙班这10名同学中随机抽取两名身高不低于173cm的同学,求身高176cm的同学被抽到的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义:如果函数![]() 在定义域内给定区间
在定义域内给定区间![]() 上存在
上存在![]() ,满足
,满足![]() ,则称函数
,则称函数![]() 是
是![]() 上的“平均值函数”,
上的“平均值函数”,![]() 是它的一个均值点.例如y=| x |是
是它的一个均值点.例如y=| x |是![]() 上的“平均值函数”,0就是它的均值点.给出以下命题:
上的“平均值函数”,0就是它的均值点.给出以下命题:
①函数![]() 是
是![]() 上的“平均值函数”.
上的“平均值函数”.
②若![]() 是
是![]() 上的“平均值函数”,则它的均值点x0≥
上的“平均值函数”,则它的均值点x0≥![]() .
.
③若函数![]() 是
是![]() 上的“平均值函数”,则实数m的取值范围是
上的“平均值函数”,则实数m的取值范围是![]() .
.
④若![]() 是区间[a.,b] (b>a.≥1)上的“平均值函数”,
是区间[a.,b] (b>a.≥1)上的“平均值函数”,![]() 是它的一个均值点,则
是它的一个均值点,则![]() .
.
其中的真命题有_________.(写出所有真命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“搜索指数”是网民通过搜索引擎,以每天搜索关键词的次数为基础所得到的统计指标.“搜索指数”越大,表示网民对该关键词的搜索次数越多,对该关键词相关的信息关注度也越高.下图是2017年9月到2018年2月这半年中,某个关键词的搜索指数变化的走势图.

根据该走势图,下列结论正确的是( )
A. 这半年中,网民对该关键词相关的信息关注度呈周期性变化
B. 这半年中,网民对该关键词相关的信息关注度不断减弱
C. 从网民对该关键词的搜索指数来看,去年10月份的方差小于11月份的方差
D. 从网民对该关键词的搜索指数来看,去年12月份的平均值大于今年1月份的平均值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com