
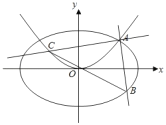
【题目】已知曲线![]() ,曲线
,曲线![]() ,且
,且![]() 与
与![]() 的焦点之间的距离为
的焦点之间的距离为![]() ,且
,且![]() 与
与![]() 在第一象限的交点为
在第一象限的交点为![]() .
.
(1)求曲线![]() 的方程和点
的方程和点![]() 的坐标;
的坐标;
(2)若过点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 与
与![]() 的另一个交点为
的另一个交点为![]() ,过点
,过点![]() 与
与![]() 垂直的直线与
垂直的直线与![]() 的另一个交点为
的另一个交点为![]() .设
.设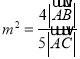 ,试求
,试求![]() 取值范围.
取值范围.
【答案】(1) ![]() ,
, ![]() (2)
(2) ![]() ,
, 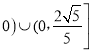
【解析】试题分析:(1)根据已知求得![]() 的焦点坐标,根据两条曲线的焦点距离列方程,可求得曲线
的焦点坐标,根据两条曲线的焦点距离列方程,可求得曲线![]() 焦点的坐标,进而求得抛物线方程.联立抛物线方程和椭圆方程,解方程组求得
焦点的坐标,进而求得抛物线方程.联立抛物线方程和椭圆方程,解方程组求得![]() 点的坐标.(2)当直线
点的坐标.(2)当直线![]() 斜率不存在时,求得
斜率不存在时,求得![]() 两点的坐标,进而求得
两点的坐标,进而求得![]() 的值.当直线
的值.当直线![]() 的斜率存在时,设出直线
的斜率存在时,设出直线![]() 的方程,联立直线的方程和椭圆的方程,解出
的方程,联立直线的方程和椭圆的方程,解出![]() 点的坐标.同理联立直线
点的坐标.同理联立直线![]() 的方程和抛物线的方程,解出
的方程和抛物线的方程,解出![]() 点的坐标,利用弦长公式求得
点的坐标,利用弦长公式求得![]() 的长度,最后求得
的长度,最后求得![]() 得取值范围.
得取值范围.
试题解析:
(1)曲线C1的焦点坐标为![]() ,曲线C2的焦点坐标为
,曲线C2的焦点坐标为![]() ,由
,由![]() 与
与![]() 的焦点之间的距离为2,得
的焦点之间的距离为2,得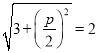 ,解得
,解得![]() ,∴
,∴![]() 的方程为
的方程为![]() .
.
由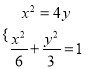 ,解得
,解得![]() ,
,
(2)当直线![]() 的斜率不存在时,
的斜率不存在时,
由题意可知, ![]() ,
, ![]() ,
, ![]() 则
则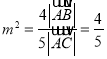 ,
,
当直线AB的斜率存在时,
∴设直线AB的方程为y﹣1=k(x﹣2),即y=kx﹣2k+1,
由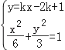 ,得(2k2+1)x+4k(1﹣2k)x+2(1﹣2k)2﹣6=0
,得(2k2+1)x+4k(1﹣2k)x+2(1﹣2k)2﹣6=0
则![]() ,∵xA=2,∴
,∵xA=2,∴![]() ,
,
又直线AC的方程为![]() ,由
,由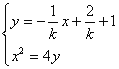 ,得
,得![]() ,则
,则![]() ,∵xA=2,∴
,∵xA=2,∴![]() ,
,
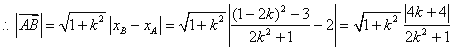 ,
,
同理![]() ,------9分
,------9分
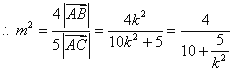 ,
,![]()
![]() -
-
即![]() .
.
![]() 综上所述:
综上所述:![]()


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】恩格尔系数(记为![]() )是指居民的食物支出占家庭消费总支出的比重.国际上常用恩格尔系数来衡量一个国家和地区人民生活水平的状况.联合国对消费水平的规定标准如下表:
)是指居民的食物支出占家庭消费总支出的比重.国际上常用恩格尔系数来衡量一个国家和地区人民生活水平的状况.联合国对消费水平的规定标准如下表:
家庭类型 | 贫穷 | 温饱 | 小康 | 富裕 | 最富裕 |
|
|
|
|
|
|
实施精准扶贫以来,根据对某山区贫困家庭消费支出情况(单位:万元)的抽样调查,2018年每个家庭平均消费支出总额为2万元,其中食物消费支出为1.2万元预测2018年到2020年每个家庭平均消费支出总额每年的增长率约是30%,而食物消费支出平均每年增加0.2万元,预测该山区的家庭2020年将处于( )
A.贫困水平B.温饱水平C.小康水平D.富裕水平
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx![]() x2,g(x)
x2,g(x)![]() x2+x,m∈R,令F(x)=f(x)+g(x).
x2+x,m∈R,令F(x)=f(x)+g(x).
(Ⅰ)求函数f(x)的单调递增区间;
(Ⅱ)若关于x的不等式F(x)≤mx﹣1恒成立,求整数m的最小值;
(Ⅲ)若m=﹣1,且正实数x1,x2满足F(x1)=﹣F(x2),求证:x1+x2![]() 1.
1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】由中央电视台综合频道(![]() )和唯众传媒联合制作的《开讲啦》是中国首档青年电视公开课,每期节目由一位知名人士讲述自己的故事,分享他们对于生活和生命的感悟,给予中国青年现实的讨论和心灵的滋养,讨论青年们的人生问题,同时也在讨论青春中国的社会问题,受到青年观众的喜爱,为了了解观众对节目的喜爱程度,电视台随机调查了
)和唯众传媒联合制作的《开讲啦》是中国首档青年电视公开课,每期节目由一位知名人士讲述自己的故事,分享他们对于生活和生命的感悟,给予中国青年现实的讨论和心灵的滋养,讨论青年们的人生问题,同时也在讨论青春中国的社会问题,受到青年观众的喜爱,为了了解观众对节目的喜爱程度,电视台随机调查了![]() 两个地区共100名观众,得到如下的
两个地区共100名观众,得到如下的![]() 列联表:
列联表:
非常满意 | 满意 | 合计 | |
|
|
| |
|
|
| |
合计 |
已知在被调查的100名观众中随机抽取1名,该观众是![]() 地区当中“非常满意”的观众的概率为0.35,且
地区当中“非常满意”的观众的概率为0.35,且![]() .
.
(1)现从100名观众中用分层抽样的方法抽取20名进行问卷调查,则应抽取“满意”的![]() 地区的人数各是多少?
地区的人数各是多少?
(2)在(1)抽取的“满意”的观众中,随机选出2人进行座谈,求至少有1名是![]() 地区观众的概率?
地区观众的概率?
(3)完成上述表格,并根据表格判断是否有90%的把握认为观众的满意程度与所在地区有关系?
附:参考公式:

| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂每月生产一种投影仪的固定成本为![]() 万元,但每生产
万元,但每生产![]() 台,需要加可变成本(即另增加投入)
台,需要加可变成本(即另增加投入)![]() 万元,市场对此产品的月需求量为
万元,市场对此产品的月需求量为![]() 台,销售的收入函数为
台,销售的收入函数为![]() (万元)
(万元)![]() 且
且![]() ,其中
,其中![]() 是产品售出的数量(单位:百台).
是产品售出的数量(单位:百台).
(1)求月销售利润![]() (万元)关于月产量
(万元)关于月产量![]() (百台)的函数解析式;
(百台)的函数解析式;
(2)当月产量为多少时,销售利润可达到最大?最大利润为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代数学名著《算法统宗》中有如下问题:“远望巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯?”意思是:一座7层塔共挂了381盏灯,且相邻两层中的下一层灯数是上一层灯数的2倍,则塔的顶层共有灯( )
A. 1盏 B. 3盏 C. 5盏 D. 9盏
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() 的离心率为
的离心率为![]() ,
, ![]() ,
, ![]() 分别为椭圆的上顶点和右焦点,
分别为椭圆的上顶点和右焦点, ![]() 的面积为
的面积为![]() ,直线
,直线![]() 与椭圆交于另一个点
与椭圆交于另一个点![]() ,线段
,线段![]() 的中点为
的中点为![]() .
.
(1)求直线![]() 的斜率;
的斜率;
(2)设平行于![]() 的直线
的直线![]() 与椭圆交于不同的两点
与椭圆交于不同的两点![]() ,
, ![]() ,且与直线
,且与直线![]() 交于点
交于点![]() ,求证:存在常数
,求证:存在常数![]() ,使得
,使得![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c.满足2acosC+bcosC+ccosB=0.
(Ⅰ)求角C的大小;
(Ⅱ)若a=2,△ABC的面积为![]() ,求C的大小。
,求C的大小。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com