
【题目】已知函数f(x)=lnx![]() x2,g(x)
x2,g(x)![]() x2+x,m∈R,令F(x)=f(x)+g(x).
x2+x,m∈R,令F(x)=f(x)+g(x).
(Ⅰ)求函数f(x)的单调递增区间;
(Ⅱ)若关于x的不等式F(x)≤mx﹣1恒成立,求整数m的最小值;
(Ⅲ)若m=﹣1,且正实数x1,x2满足F(x1)=﹣F(x2),求证:x1+x2![]() 1.
1.
【答案】(Ⅰ)(0,1);(Ⅱ)2;(Ⅲ)详见解析.
【解析】
(I)先求得函数的定义域,然后利用导数求出函数的单调递增区间.(II)构造函数![]() ,利用导数求得
,利用导数求得![]() 的最大值,这个最大值恒为非负数,由此求得整数
的最大值,这个最大值恒为非负数,由此求得整数![]() 的最小值.(III)当
的最小值.(III)当![]() 时,
时,![]() ,化简
,化简![]() ,利用构造函数法以及导数求其最小值,证得
,利用构造函数法以及导数求其最小值,证得![]()
解:(Ⅰ)f(x)的定义域为:{x|x>0},
f′(x)![]() x
x![]() ,(x>0),
,(x>0),
由f′(x)>0,得:0<x<1,
所以f(x)的单调递增区间为(0,1).
(Ⅱ)F(x)=f(x)+g(x)=lnx![]() mx2+x,x>0,
mx2+x,x>0,
令G(x)=F(x)﹣(mx﹣1)=lnx![]() mx2+(1﹣m)x+1,
mx2+(1﹣m)x+1,
则不等式F(x)≤mx﹣1恒成立,即G(x)≤0恒成立.
G′(x)![]() mx+(1﹣m)
mx+(1﹣m)![]() ,
,
①当m≤0时,因为x>0,所以G′(x)>0
所以G(x)在(0,+∞)上是单调递增函数,
又因为G(1)=ln1![]() m×12+(1﹣m)+1
m×12+(1﹣m)+1![]() m+2>0,
m+2>0,
所以关于x的不等式G(x)≤0不能恒成立,
②当m>0时,G′(x)![]() ,
,
令G′(x)=0,因为x>0,得x![]() ,
,
所以当x∈(0,![]() )时,G′(x)>0;当x∈(
)时,G′(x)>0;当x∈(![]() ,+∞)时,G′(x)<0,
,+∞)时,G′(x)<0,
因此函数G(x)在x∈(0,![]() )是增函数,在x∈(
)是增函数,在x∈(![]() ,+∞)是减函数,
,+∞)是减函数,
故函数G(x)的最大值为:
G(![]() )=ln
)=ln![]() m
m![]() (1﹣m)
(1﹣m)![]() 1
1![]() lnm,
lnm,
令h(m)![]() lnm,因为h(m)在m∈(0,+∞)上是减函数,
lnm,因为h(m)在m∈(0,+∞)上是减函数,
又因为h(1)![]() 0,h(2)
0,h(2)![]() ln2<0,所以当m≥2时,h(m)<0,
ln2<0,所以当m≥2时,h(m)<0,
所以整数m的最小值为2.
(Ⅲ)m=﹣1时,F(x)=lnx![]() x2+x,x>0,
x2+x,x>0,
由F(x1)=﹣F(x2),得F(x1)+F(x2)=0,即lnx1![]() x1+lnx2
x1+lnx2![]() x2=0,
x2=0,
整理得:![]() (x1+x2)=x1 x2﹣ln(x1 x2),
(x1+x2)=x1 x2﹣ln(x1 x2),
令t=x1x2>0,则由φ(t)=t﹣lnt,得:φ′(t)![]() ,
,
可知φ(t)在区间(0,1)上单调递减,在区间(1,+∞)上单调递增,
所以φ(t)≥φ(1)=1,
所以![]() (x1+x2)≥1,解得:x1+x2
(x1+x2)≥1,解得:x1+x2![]() 1,或x1+x2
1,或x1+x2![]() 1,
1,
因为x1,x2为正整数,所以:x1+x2![]() 1成立.
1成立.


科目:高中数学 来源: 题型:
【题目】某城市在进行创建文明城市的活动中,为了解居民对“创文”的满意程度,组织居民给活动打分(分数为整数.满分为100分).从中随机抽取一个容量为120的样本.发现所有数据均在![]() 内.现将这些分数分成以下6组并画出了样本的频率分布直方图,但不小心污损了部分图形,如图所示.观察图形,回答下列问题:
内.现将这些分数分成以下6组并画出了样本的频率分布直方图,但不小心污损了部分图形,如图所示.观察图形,回答下列问题:
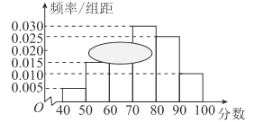
(1)算出第三组![]() 的频数.并补全频率分布直方图;
的频数.并补全频率分布直方图;
(2)请根据频率分布直方图,估计样本的众数、中位数和平均数.(每组数据以区间的中点值为代表)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l1:x+2y+1=0,l2:-2x+y+2=0,它们相交于点A.
(1)判断直线l1和l2是否垂直?请给出理由.
(2)求过点A且与直线l3:3x+y+4=0平行的直线方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列各一元二次不等式中,解集为空集的是( )
A.(x+3)(x﹣1)>0B.(x+4)(x﹣1)<0
C.x2﹣2x+3<0D.2x2﹣3x﹣2>0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的焦距为
的焦距为![]() ,其短轴的两个端点与长轴的一个端点构成正三角形.
,其短轴的两个端点与长轴的一个端点构成正三角形.
(Ⅰ)求椭圆![]() 的标准方程和长轴长;
的标准方程和长轴长;
(Ⅱ)设![]() 为椭圆
为椭圆![]() 的左焦点,
的左焦点, ![]() 为直线
为直线![]() 上任意一点,过点
上任意一点,过点![]() 作直线
作直线![]() 的垂线交椭圆
的垂线交椭圆![]() 于
于![]() ,记
,记![]() 分别为点
分别为点![]() 和
和![]() 到直线
到直线![]() 的距离,证明
的距离,证明![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
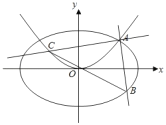
【题目】已知曲线![]() ,曲线
,曲线![]() ,且
,且![]() 与
与![]() 的焦点之间的距离为
的焦点之间的距离为![]() ,且
,且![]() 与
与![]() 在第一象限的交点为
在第一象限的交点为![]() .
.
(1)求曲线![]() 的方程和点
的方程和点![]() 的坐标;
的坐标;
(2)若过点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 与
与![]() 的另一个交点为
的另一个交点为![]() ,过点
,过点![]() 与
与![]() 垂直的直线与
垂直的直线与![]() 的另一个交点为
的另一个交点为![]() .设
.设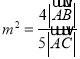 ,试求
,试求![]() 取值范围.
取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在贯彻中共中央国务院关于精准扶贫政策的过程中,某单位定点帮扶甲、乙两个村各50户贫困户.为了做到精准帮扶,工作组对这100户村民的年收入情况、劳动能力情况、子女受教育情况、危旧房情况、患病情况等进行调查,并把调查结果转化为各户的贫困指标![]() 和
和![]() ,制成下图,其中“
,制成下图,其中“![]() ”表示甲村贫困户,“
”表示甲村贫困户,“![]() ”表示乙村贫困户.若
”表示乙村贫困户.若![]() ,则认定该户为“绝对贫困户”,若
,则认定该户为“绝对贫困户”,若![]() ,则认定该户为“相对贫困户”,若
,则认定该户为“相对贫困户”,若![]() ,则认定该户为“低收入户”;若
,则认定该户为“低收入户”;若![]() ,则认定该户为“今年能脱贫户”,否则为“今年不能脱贫户”.
,则认定该户为“今年能脱贫户”,否则为“今年不能脱贫户”.
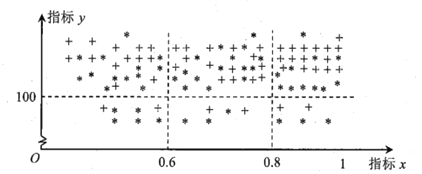
(1)从乙村的50户中随机选出一户,求该户为“绝对贫困户”的概率;
(2)从甲村所有“今年不能脱贫的非绝对贫困户”中任选2户,求选出的2户均为“低收入户”的概率;
(3)试比较这100户中,甲、乙两村指标![]() 的方差的大小(只需写出结论).
的方差的大小(只需写出结论).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com