
【题目】定义:如果函数![]() 在定义域内给定区间
在定义域内给定区间![]() 上存在
上存在![]() ,满足
,满足![]() ,则称函数
,则称函数![]() 是
是![]() 上的“平均值函数”,
上的“平均值函数”,![]() 是它的一个均值点.例如y=| x |是
是它的一个均值点.例如y=| x |是![]() 上的“平均值函数”,0就是它的均值点.给出以下命题:
上的“平均值函数”,0就是它的均值点.给出以下命题:
①函数![]() 是
是![]() 上的“平均值函数”.
上的“平均值函数”.
②若![]() 是
是![]() 上的“平均值函数”,则它的均值点x0≥
上的“平均值函数”,则它的均值点x0≥![]() .
.
③若函数![]() 是
是![]() 上的“平均值函数”,则实数m的取值范围是
上的“平均值函数”,则实数m的取值范围是![]() .
.
④若![]() 是区间[a.,b] (b>a.≥1)上的“平均值函数”,
是区间[a.,b] (b>a.≥1)上的“平均值函数”,![]() 是它的一个均值点,则
是它的一个均值点,则![]() .
.
其中的真命题有_________.(写出所有真命题的序号)
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中,![]() ,底面
,底面![]() 为直角梯形,
为直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() 为线段
为线段![]() 上一点.
上一点.
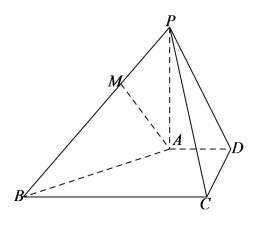
(I)若![]() ,求证:
,求证:![]() 平面
平面![]() ;
;
(II)若![]() ,
,![]() ,异面直线
,异面直线![]() 与
与![]() 成
成![]() 角,二面角
角,二面角![]() 的余弦值为
的余弦值为![]() ,求
,求![]() 的长及直线
的长及直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂生产的产品中分正品与次品,正品重![]() ,次品重
,次品重![]() ,现有5袋产品(每袋装有10个产品),已知其中有且只有一袋次品(10个产品均为次品)如果将5袋产品以1~5编号,第
,现有5袋产品(每袋装有10个产品),已知其中有且只有一袋次品(10个产品均为次品)如果将5袋产品以1~5编号,第![]() 袋取出
袋取出![]() 个产品(
个产品(![]() ),并将取出的产品一起用秤(可以称出物体重量的工具)称出其重量
),并将取出的产品一起用秤(可以称出物体重量的工具)称出其重量![]() ,若次品所在的袋子的编号是2,此时的重量
,若次品所在的袋子的编号是2,此时的重量![]() _________
_________![]() ;若次品所在的袋子的编号是
;若次品所在的袋子的编号是![]() ,此时的重量
,此时的重量![]() _______
_______![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为坐标原点,点
为坐标原点,点![]() 在圆
在圆![]() :
:![]() 上.
上.
(1)求实数![]() 的值;
的值;
(2)求过圆心![]() 且与直线
且与直线![]() 平行的直线的方程;
平行的直线的方程;
(3)过点![]() 作互相垂直的直线
作互相垂直的直线![]() ,
,![]() ,
,![]() 与圆
与圆![]() 交于
交于![]() 两点,
两点,![]() 与圆
与圆![]() 交于
交于![]() 两点,求
两点,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】质检部门为了解某企业生产的一-种圆柱形零件的质量情况,随机抽检了100个零件,得到这些零件的横截面直径d(单位:![]() )的频率分布表如下:
)的频率分布表如下:
d的分组 |
|
|
|
|
|
零件数 | 12 | 38 | 38 | 10 | 2 |
(1)试估计这个企业生产的这类零件的横截面直径不低于![]() 的概率;
的概率;
(2)求这个企业生产的这类零件的横截面直径的平均数与标准差的估计值(同一组中的数据用该区间的中点值为代表).(精确到0.01)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com