练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知为坐标原点,点在圆:上.

    （1）求实数的值；

    （2）求过圆心且与直线平行的直线的方程；

    （3）过点作互相垂直的直线,,与圆交于两点,与圆交于两点,求的最大值．

    【答案】（1）（2）（3）

    【解析】

    （1）点在圆:上,即可求得答案;

    （2）直线的斜率为,圆以的圆心为,因为过圆心且与直线平行的直线的方程为:,即可求得答案;

    （3）设直线的方程为,则的方程为,求出圆心到直线的距离和圆心到直线的距离,即可和,结合已知,根据均值不等式,即可求得答案.

    （1）点在圆:上

    解得:

    （2）直线的斜率为,圆的圆心为

    过圆心且与直线平行的直线的方程为:

    即

    （3）圆的标准方程为:

    故直线的斜率均存在.

    设直线的方程为,则的方程为

    于是圆心到直线的距离为:

    圆心到直线的距离为

    又由可得的取值范围是

    此时:

    当且仅当即时取等号

    的最大值为

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图所示，在四棱锥中，底面是菱形，，与交于点，底面，为的中点，.

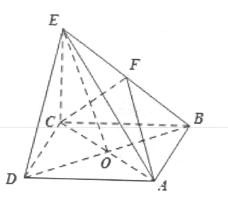
    （1）求证： 平面；

    （2）求异面直线与所成角的余弦值；

    （3）求与平面所成角的正弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】随机抽取某中学甲、乙两班各10名同学，测量他们的身高（单位：cm），获得身高数据的茎叶图如图所示.

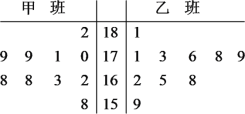
    （1）试比较甲、乙两班分别抽取的这10名同学身高的中位数大小；

    （2）现从乙班这10名同学中随机抽取两名身高不低于173cm的同学，求身高176cm的同学被抽到的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】定义：如果函数在定义域内给定区间上存在，满足，则称函数是上的“平均值函数”，是它的一个均值点．例如y=| x |是上的“平均值函数”，0就是它的均值点．给出以下命题：

    ①函数是上的“平均值函数”．

    ②若是上的“平均值函数”，则它的均值点x0≥．

    ③若函数是上的“平均值函数”，则实数m的取值范围是．

    ④若是区间[a.，b] （b>a.≥1）上的“平均值函数”，是它的一个均值点，则．

    其中的真命题有_________．（写出所有真命题的序号）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）讨论的单调性；

    （2）如果方程有两个不相等的解，且，证明：.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列{an}满足：a1＝，an＋1＝（n∈N*）．（其中e为自然对数的底数，e＝2.71828…）

    （1）证明：an＋1>an（n∈N*）；

    （2）设bn＝1－an，是否存在实数M>0，使得b1＋b2＋…＋bn≤M对任意n∈N*成立？若存在，求出M的一个值；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，已知六个直角边均为1和的直角三角形围成的两个正六边形，则该图形绕着旋转一周得到的几何体的体积为（ ）

    A.B.C.D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某学校为了解本校文、理科学生的学业水平模拟测试数学成绩情况，分别从理科班学生中随机抽取人的成绩得到样本甲，从文科班学生中随机抽取人的成绩得到样本乙，根据两个样本数据分别得到如下直方图：

    甲样本数据直方图

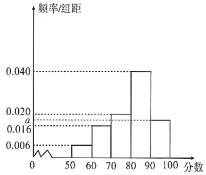
    乙样本数据直方图

    已知乙样本中数据在的有个.

    （1）求和乙样本直方图中的值；

    （2）试估计该校理科班学生本次模拟测试数学成绩的平均值和文科班学生本次模拟测试数学成绩的中位数（同一组中的数据用该组区间中点值为代表）.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在衡阳市“创全国文明城市”（简称“创文”）活动中，市教育局对本市A，B，C，D四所高中学校按各校人数分层抽样，随机抽查了200人，将调查情况进行整理后制成下表：

    学校

    A

    B

    C

    D

    抽查人数

    10

    15

    100

    75

    “创文”活动中参与的人数

    9

    10

    80

    49

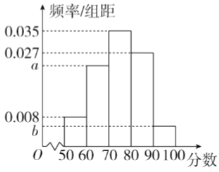
    假设每名高中学生是否参与“创文”活动是相互独立的

    （1）若本市共8000名高中学生，估计C学校参与“创文”活动的人数；

    （2）在上表中从A，B两校没有参与“创文”活动的同学中随机抽取2人，求恰好A，B两校各有1人没有参与“创文”活动的概率；

    （3）在随机抽查的200名高中学生中，进行文明素养综合素质测评（满分为100分），得到如上的频率分布直方图，其中．求a，b的值，并估计参与测评的学生得分的中位数．（计算结果保留两位小数）．

    查看答案和解析>>

    同步练习册答案