
【题目】如图,已知平行四边形ABCD中,BC=6,正方形ADEF所在平面与平面ABCD垂直,G,H分别是DF,BE的中点.
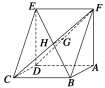
(1)求证:GH∥平面CDE;
(2)若CD=2,DB=4![]() ,求四棱锥F—ABCD的体积.
,求四棱锥F—ABCD的体积.
【答案】(1)见解析 (2)16![]()
【解析】(1)证明 方法一 ∵EF∥AD,AD∥BC,∴EF∥BC.
又EF=AD=BC,∴四边形EFBC是平行四边形,
∴H为FC的中点.
又∵G是FD的中点,∴HG∥CD.
∵HG平面CDE,CD平面CDE,
∴GH∥平面CDE.

方法二 连接EA,∵ADEF是正方形,
∴G是AE的中点.
∴在△EAB中,GH∥AB.
又∵AB∥CD,∴GH∥CD.
∵HG平面CDE,CD平面CDE,
∴GH∥平面CDE.
(2)解 ∵平面ADEF⊥平面ABCD,交线为AD,
且FA⊥AD,∴FA⊥平面ABCD.
∵AD=BC=6,∴FA=AD=6.
又∵CD=2,DB=4![]() ,CD2+DB2=BC2,∴BD⊥CD.
,CD2+DB2=BC2,∴BD⊥CD.
∵SABCD=CD·BD=8![]() ,
,
∴VF—ABCD=![]() SABCD·FA=
SABCD·FA=![]() ×8
×8![]() ×6=16
×6=16![]() .
.


 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:高中数学 来源: 题型:
【题目】2016年1月2日凌晨某公司公布的元旦全天交易数据显示,天猫元旦当天全天的成交金额为315.5亿元.为了了解网购者一次性购物情况,某统计部门随机抽查了1月1日100名网购者的网购情况,得到如下数据统计表,已知网购金额在2000元以上(不含2000元)的频率为0.4.
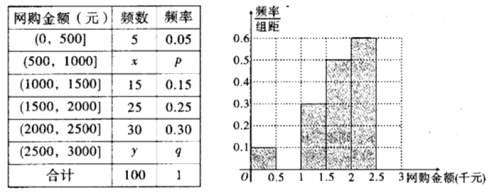
(I)先求出![]() 的值,再将如图4所示的频率分布直方图绘制完整;
的值,再将如图4所示的频率分布直方图绘制完整;
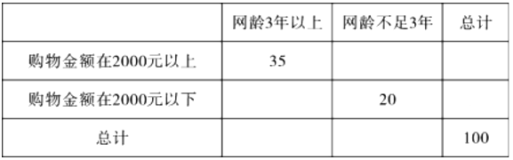
(II)对这100名网购者进一步调查显示:购物金额在2000元以上的购物者中网龄3年以上的有35人,
购物金额在2000元以下(含2000元)的购物者中网龄不足3年的有20人,请填写下面的列联表,并据
此判断能否在犯错误的概率不超过0.025的前提下认为网购金额超过2000元与网龄在3年以上有关?
参考数据:

参考公式:![]() ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,
(1)当![]() 时,证明:函数
时,证明:函数![]() 不是奇函数;
不是奇函数;
(2)判断函数![]() 的单调性,并利用函数单调性的定义给出证明;
的单调性,并利用函数单调性的定义给出证明;
(3)若![]() 是奇函数,且
是奇函数,且![]() 在
在![]() 时恒成立,求实数
时恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() ,
,![]() .
.
(1)若函数![]() 在
在![]() 处有极值,求函数
处有极值,求函数![]() 的最大值;
的最大值;
(2)①是否存在实数![]() ,使得关于
,使得关于![]() 的不等式
的不等式![]() 在
在![]() 上恒成立?若存在,求出
上恒成立?若存在,求出![]() 的取值范围;若不存在,说明理由;
的取值范围;若不存在,说明理由;
②证明:不等式![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,点
,点![]() 也为抛物线
也为抛物线![]() 的焦点,过点
的焦点,过点![]() 的直线
的直线![]() 交抛物线
交抛物线![]() 于
于![]() 两点.
两点.
(Ⅰ)若点![]() 满足
满足![]() ,求直线
,求直线![]() 的方程;
的方程;
(Ⅱ)![]() 为直线
为直线![]() 上任意一点,过点
上任意一点,过点![]() 作
作![]() 的垂线交椭圆
的垂线交椭圆![]() 于
于![]() 两点,求
两点,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知点
中,已知点![]()
![]() 为平面上的动点,且过点
为平面上的动点,且过点![]() 作
作![]() 的垂线,垂足为
的垂线,垂足为![]() ,满足:
,满足:![]()
(Ⅰ)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)在轨迹![]() 上求一点
上求一点![]() ,使得
,使得![]() 到直线
到直线![]() 的距离最短,并求出最短距离.
的距离最短,并求出最短距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C的标准方程是![]()
(Ⅰ)求它的焦点坐标和准线方程;
(Ⅱ)直线![]() 过已知抛物线C的焦点且倾斜角为45°,且与抛物线的交点为A、B,求线段AB的长度.
过已知抛物线C的焦点且倾斜角为45°,且与抛物线的交点为A、B,求线段AB的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等比数列{an}的公比q>1,且满足a2+a3+a4=28,且a3+2是a2,a4的等差中项.
(1)求数列{an}的通项公式;
(2)若bn=log![]() ,Sn=b1+b2+…+bn,求使
,Sn=b1+b2+…+bn,求使![]() 成立的正整数n的最大值.
成立的正整数n的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com