练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    6．下列说法错误的是（　　）
    A．若棱柱的底面边长相等，则它的各个侧面的面积相等
    B．九棱柱有9条侧棱，9个侧面，侧面为平行四边形
    C．六角螺帽、三棱镜的外形都是棱柱
    D．正四棱台的侧面不一定是等腰梯形

    分析 若棱柱的底面边长相等，则它的各个侧面是全等的平行四边形；由棱柱的定义能判断B的对错；六角螺帽的外形是六棱柱，三棱镜的外形是三棱柱；用正四棱台的定义能判断D的对错．

    解答 解：在A中：若棱柱的底面边长相等，则它的各个侧面是全等的平行四边形，故面积相等，A正确；
    在B中：由棱柱的定义知九棱柱有9条侧棱，9个侧面，侧面为平行四边形，B正确；
    在C中：六角螺帽的外形是六棱柱，三棱镜的外形是三棱柱，C正确；
    在D中：正四棱台的侧面一定是等腰梯形，故D错误．
    故选：D．

    点评 本题考查命题真假的判断，是基础题，解题时要注意棱柱、棱台的定义和性质的合理运用．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

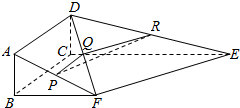    16．如图，四边形ABCD是矩形，四边形BCEF是直角梯形，平面ABCD⊥平面BCEF，∠FBC是直角，AB=1，BC=BF=2，CE=4，P、Q、R分别是AF、DF、DE的中点．
    （1）求证：PQ∥平面BCEF；
    （2）求二面角P-QR-E的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

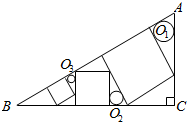    17．△ABC中，∠C=90°，作三个正方形及三个圆O1，O2，O3，如图，半径分别为r1，r2，r3．证明：r1r3=r${\;}_{2}^{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    14．某几何体的三视图如图所示，该几何体的表面积为（　　）
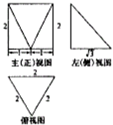
    A．12+$\sqrt{3}+\sqrt{7}$B．4+3$\sqrt{3}+\sqrt{7}$C．8+$\sqrt{3}+\sqrt{7}$D．4+$\sqrt{3}+\sqrt{7}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

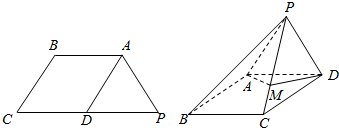    1．已知梯形ABCP，如图（1）所示，D是CP边的中点，AB∥PC，且2AB=PC，△APD为等边三角形，现将平面APD沿AD翻折，使平面APD⊥平面ABCD，得到如图（2）所示的四棱锥P-ABCD，点M在棱PC上，且PM=$\sqrt{3}$MC．
    （1）证明：AD⊥PB；
    （2）求二面角P-AD-M的大小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

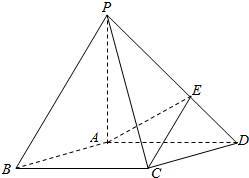    11．如图，在底面是菱形的四棱锥P-ABCD中，∠ABC=60°，PA=AC=a，PB=PD=$\sqrt{2}$a，点E是PD的中点．
    （1）证明：平面PBD⊥平面PAC；
    （2）求二面角E-AC-D的正切值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

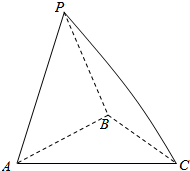    18．如图所示的三棱锥P-ABC的三条侧棱两两垂直，且PB=1，PA=$\sqrt{3}$，PC=$\sqrt{6}$．
    （1）求其体积．（一直线和一平面内两相交直线垂直，则直线与平面垂直）
    （2）求点P到面ABC的距离．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．从空间一点P向二面角α-l-β的两个面α、β分别作垂线PE、PF，E，F分别为垂足，若∠EPF=40°，则二面角的平面角的大小是（　　）
    A．40°B．40°或140°C．140°D．50°

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    16．求下列函数的导数
    （1）y=x$\sqrt{1+{x}^{2}}$
    （2）y=xcos（2x+$\frac{π}{2}$）sin（2x+$\frac{π}{2}$）

    查看答案和解析>>

    同步练习册答案