
【题目】某种热饮需用开水冲泡,其基本操作流程如下:①先将水加热到100![]() ,水温
,水温![]() 与时间
与时间![]() 近似满足一次函数关系;②用开水将热饮冲泡后在室温下放置,温度
近似满足一次函数关系;②用开水将热饮冲泡后在室温下放置,温度![]() 与时间
与时间![]() 近似满足函数的关系式为
近似满足函数的关系式为 ![]() (
(![]() 为常数), 通常这种热饮在40
为常数), 通常这种热饮在40![]() 时,口感最佳,某天室温为
时,口感最佳,某天室温为![]() 时,冲泡热饮的部分数据如图所示,那么按上述流程冲泡一杯热饮,并在口感最佳时饮用,最少需要的时间为
时,冲泡热饮的部分数据如图所示,那么按上述流程冲泡一杯热饮,并在口感最佳时饮用,最少需要的时间为

A. 35![]() B. 30
B. 30![]()
C. 25![]() D. 20
D. 20![]()
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】如图,在四棱锥S-ABCD中,![]() 平面
平面![]() ,底面ABCD为直角梯形,
,底面ABCD为直角梯形,![]() ,
,![]() ,且
,且![]()
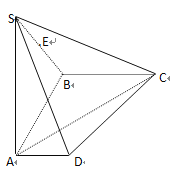
(Ⅰ)求![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
(Ⅱ)若E为SB的中点,在平面![]() 内存在点N,使得
内存在点N,使得![]() 平面
平面![]() ,求N到直线AD,SA的距离.
,求N到直线AD,SA的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)是定义在(-2,2)上的奇函数.当x∈(-2,0)时,f(x)=-loga(-x)-loga(2+x),其中a>1.
(1)求函数f(x)的零点.
(2)若t∈(0,2),判断函数f(x)在区间(0,t]上是否有最大值和最小值.若有,请求出最大值和最小值,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某地区2008年至2014年中,每年的居民人均纯收入y(单位:千元)的数据如下表:
年份 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 |
年份代号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
人均纯收入 | 2.7 | 3.6 | 3.3 | 4.6 | 5.4 | 5.7 | 6.2 |
对变量![]() 与
与![]() 进行相关性检验,得知
进行相关性检验,得知![]() 与
与![]() 之间具有线性相关关系.
之间具有线性相关关系.
(1)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)预测该地区2017年的居民人均纯收入.
附:回归直线的斜率和截距的最小二乘估计公式分别为: ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为迎接![]() 年北京冬季奥运会,普及冬奥知识,某校开展了“冰雪答题王”冬奥知识竞赛活动.现从参加冬奥知识竞赛活动的学生中随机抽取了
年北京冬季奥运会,普及冬奥知识,某校开展了“冰雪答题王”冬奥知识竞赛活动.现从参加冬奥知识竞赛活动的学生中随机抽取了![]() 名学生,将他们的比赛成绩(满分为
名学生,将他们的比赛成绩(满分为![]() 分)分为
分)分为![]() 组:
组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,得到如图所示的频率分布直方图.
,得到如图所示的频率分布直方图.

(Ⅰ)求![]() 的值;
的值;
(Ⅱ)记![]() 表示事件“从参加冬奥知识竞赛活动的学生中随机抽取一名学生,该学生的比赛成绩不低于
表示事件“从参加冬奥知识竞赛活动的学生中随机抽取一名学生,该学生的比赛成绩不低于![]() 分”,估计
分”,估计![]() 的概率;
的概率;
(Ⅲ)在抽取的![]() 名学生中,规定:比赛成绩不低于
名学生中,规定:比赛成绩不低于![]() 分为“优秀”,比赛成绩低于
分为“优秀”,比赛成绩低于![]() 分为“非优秀”.请将下面的
分为“非优秀”.请将下面的![]() 列联表补充完整,并判断是否有
列联表补充完整,并判断是否有![]() 的把握认为“比赛成绩是否优秀与性别有关”?
的把握认为“比赛成绩是否优秀与性别有关”?
优秀 | 非优秀 | 合计 | |
男生 |
| ||
女生 |
| ||
合计 |
|
参考公式及数据:![]() ,
,![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在极坐标系中,直线![]() 的极坐标方程为
的极坐标方程为![]() ,现以极点
,现以极点![]() 为原点,极轴为
为原点,极轴为![]() 轴的非负半轴建立平面直角坐标系,曲线
轴的非负半轴建立平面直角坐标系,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).
为参数).
(1)求直线![]() 的直角坐标方程和曲线
的直角坐标方程和曲线![]() 的普通方程;
的普通方程;
(2)若曲线![]() 为曲线
为曲线![]() 关于直线
关于直线![]() 的对称曲线,点
的对称曲线,点![]() 分别为曲线
分别为曲线![]() 、曲线
、曲线![]() 上的动点,点
上的动点,点![]() 坐标为
坐标为![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P-ABCD中,PA⊥底面ABCD,AD∥BC,AB=AD=AC=3,PA=BC=4,M为线段AD上一点,AM=2MD,N为PC的中点.

(Ⅰ)证明MN∥平面PAB;
(Ⅱ)求四面体N-BCM的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设关于某产品的明星代言费![]() (百万元)和其销售额
(百万元)和其销售额![]() (百万元),有如下表的统计表格:
(百万元),有如下表的统计表格:
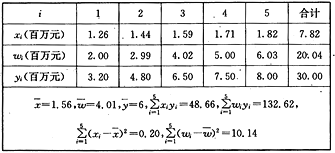
 表中
表中![]()
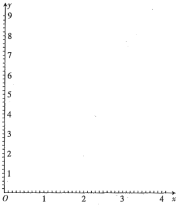
(1)在给出的坐标系![]() 中,作出销售额
中,作出销售额![]() 关于广告费
关于广告费![]() 的回归方程的散点图,根据散点图指出:
的回归方程的散点图,根据散点图指出:![]() 哪一个适合作销售额
哪一个适合作销售额![]() 关于明星代言费
关于明星代言费![]() 的回归方程(不需要说明理由);并求
的回归方程(不需要说明理由);并求![]() 关于
关于![]() 的回归方程(结果精确到0.1)
的回归方程(结果精确到0.1)
(2)已知这种产品的纯收益![]() (百万元)与
(百万元)与![]() ,
,![]() 有如下关系:
有如下关系:![]() ,用(1)中的结果估计当
,用(1)中的结果估计当![]() 取何值时,纯收益
取何值时,纯收益![]() 取最大值?
取最大值?
附:对于一组数据![]() 其回归线
其回归线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为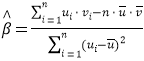 ,
,![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com