由动点P引圆x2+y2=10的两条切线PA,PB,直线PA、PB的斜率分别为k1、k2.
(1)若k1+k2+k1k2=-1,求动点P的轨迹;
(2)若点P在x+y=m上,且PA⊥PB,求实数m的取值范围.
分析:(1)设出点P的坐标,待定系数法给出切线的方程,与圆的方程联立,消元得到关于k的一元二次方程,然后用根与系数的关系即可得到k
1+k
2与k
1k
2代入k
1+k
2+k
1k
2=-1即可得到点P的坐标满足的轨迹方程.、
(2)点P(x
0、y
0)在x+y=m上,所以y
0=m-x
0.又PA⊥PB,所以,k
1k
2=-1由上题的结论知
=-1再将y
0=m-x
0代入即得关于m的方程,此方程有根,故可有判别式求出实数m的取值范围.
解答:解:(1)设P(x
0、y
0),
则|x
0|
≠,且x
02+y
02≠10,切线l:y-y
0=k(x-x
0).
由l与圆相切,得
=.
化简整理得(x
02-10)k
2-2x
0y
0k+y
02-10=0.
由韦达定理及k
1+k
2+k
1k
2=-1,得
+=-1,化简得x
0+y
0=±2
.
即P点的轨迹方程为x+y±2
=0且|x
0|
≠.即两条直线上各去掉一个点
(2)因为,点P(x
0、y
0)在x+y=m上,所以y
0=m-x
0.又PA⊥PB,
所以,k
1k
2=-1,即
=-1,将y
0=m-x
0代入化简得2x
02-2mx
0+m
2-20=0.
由△≥0,得
-2≤m≤2.经检验,m的取值范围为
[-2,2].
点评:本题考查直线与圆的位置关系,求解第一问的关键是得到关于两个斜率的一元二次方程,从而得到点P的坐标满足的方程,第二问解题的关键是得到关于参数m的方程,通过所得的方程有解得到参数m的不等式解出其范围,本题考查了转化化归的思想,做题时要注意此类思想的使用.



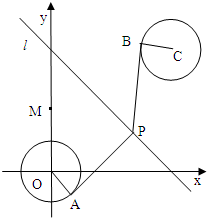 已知圆O:x2+y2=1,圆C:(x-4)2+(y-4)2=1,由两圆外一点P(a,b)引两圆切线PA、PB,切点分别为A、B,如图,满足|PA|=|PB|;
已知圆O:x2+y2=1,圆C:(x-4)2+(y-4)2=1,由两圆外一点P(a,b)引两圆切线PA、PB,切点分别为A、B,如图,满足|PA|=|PB|;