考点:直线与平面所成的角,直线与平面垂直的判定
专题:空间位置关系与距离
分析:(Ⅰ)由题意先推导出A1C1⊥平面AA1B1B,从而得到A1C1⊥AB1,由此能够证明AB1⊥平面A1BC1.
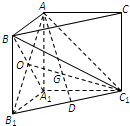
(Ⅱ) 设AB1与A1B相交于点O,由题设条件推导出AD与C1O的交点为重心G,连接OG,能推导出∠AGO是AD与平面A1BC1所成的角,由此能求出AD与平面A1BC1所成的角的大小.
解答:
解:(Ⅰ)由题意知四边形AA
1B
1B是正方形,
∴AB
1⊥BA
1.
∵AA
1⊥平面A
1B
1C
1,∴AA
1⊥A
1C
1.
又∵A
1C
1⊥A
1B
1,∴A
1C
1⊥平面AA
1B
1B,
∴A
1C
1⊥AB
1.
∴AB
1⊥平面A
1BC
1.…(7分)
(Ⅱ) 设AB
1与A
1B相交于点O,则点O是线段AB
1的中点.
连接AC
1,由题意知△AB
1C
1是正三角形.
由AD,C
1O是△AB
1C
1的中线知:AD与C
1O的交点为重心G,连接OG.
由(Ⅰ) 知AB
1⊥平面A
1BC
1,
∴OG是AD在平面A
1BC
1上的射影,
∴∠AGO是AD与平面A
1BC
1所成的角.
在直角△AOG中,
AG=
AD=
AB
1=
AB,AO=
AB,
∴sin∠AGO=
=
.
∴∠AGO=60°,
即AD与平面A
1BC
1所成的角为60°.…(15分)
点评:本题主要考查空间线、面位置关系,线面所成的角等基础知识,同时考查空间想象能力和推理论证能力.

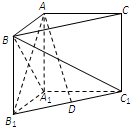 如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=AA1.
如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=AA1.


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案