
| 3 |
| p |
| 2 |
| p |
| 2 |
| 3 |
| 3 |
| 3 |
| 2 |
| 3 |
| 3 |
| 2 |
| ||
| 2 |
| 3 |
|
2±2
| ||
| k |
2+2
| ||
| k |
| 3 |
| 3 |
| 1 |
| 3 |
2
| ||
| 3 |
| 3 |
| 3 |
| 16 |
| 3 |
| 3 |
| 1 |
| 2 |
16
| ||
| 3 |


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
 坚持锻炼一小时,健康成长每一天.某校为调查高中学生在校参加体育活动的时间,随机抽取了100名高中学生进行调查,其中女学生有55名.上面是根据调查结果绘制的学生日均体育锻炼时间的频率分布直方图:
坚持锻炼一小时,健康成长每一天.某校为调查高中学生在校参加体育活动的时间,随机抽取了100名高中学生进行调查,其中女学生有55名.上面是根据调查结果绘制的学生日均体育锻炼时间的频率分布直方图:| 非良好 | 良好 | 合计 | |
| 男生 | |||
| 女生 | |||
| 合计 |
| n(ad-c)2 |
| (a+b)(c+d)(a+c)(b+d) |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,四棱锥P-ABCD中,底面ABCD为正方形,PD⊥平面ABCD,PD=AB=4,E、F、G分别是PC、PD、BC的中点.
如图,四棱锥P-ABCD中,底面ABCD为正方形,PD⊥平面ABCD,PD=AB=4,E、F、G分别是PC、PD、BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:
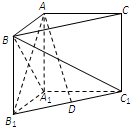 如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=AA1.
如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=AA1.查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
| 3 |
| 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:
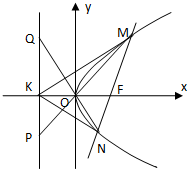 如图,已知抛物线y2=4x的焦点为F,过F的直线交抛物线于M、N两点,其准线l与x轴交于K点.
如图,已知抛物线y2=4x的焦点为F,过F的直线交抛物线于M、N两点,其准线l与x轴交于K点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com