
【题目】已知函数f(x)=|x+m|+|2x-1|.
(1)当m=-1时,求不等式f(x)≤2的解集;
(2)若f(x)≤|2x+1|的解集包含![]() ,求m的取值范围.
,求m的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)零点分段法分类讨论解绝对值不等式即可.
(2)由题意可知f(x)≤|2x+1|在![]() 上恒成立,可去掉绝对值|x+m|≤2,解绝对值不等式,结合不等式的解集即可求解.
上恒成立,可去掉绝对值|x+m|≤2,解绝对值不等式,结合不等式的解集即可求解.
(1)当m=-1时,f(x)=|x-1|+|2x-1|,
当x≥1时,f(x)=3x-2≤2,所以1≤x≤![]() ;
;
当![]() <x<1时,f(x)=x≤2,所以
<x<1时,f(x)=x≤2,所以![]() <x<1;
<x<1;
当x≤![]() 时,f(x)=2-3x≤2,所以0≤x≤
时,f(x)=2-3x≤2,所以0≤x≤![]() ,
,
综上可得原不等式f(x)≤2的解集为![]() .
.
(2)由题意可知f(x)≤|2x+1|在![]() 上恒成立,
上恒成立,
当x∈![]() 时,f(x)=|x+m|+|2x-1|=|x+m|+2x-1≤|2x+1|=2x+1,所以|x+m|≤2,
时,f(x)=|x+m|+|2x-1|=|x+m|+2x-1≤|2x+1|=2x+1,所以|x+m|≤2,
即-2≤x+m≤2,则-2-x≤m≤2-x,且(-2-x)max=-![]() ,(2-x)min=0,
,(2-x)min=0,
因此m的取值范围为![]() .
.


科目:高中数学 来源: 题型:
【题目】2017年春节期间,某服装超市举办了一次有奖促销活动,消费每超过600元(含600元),均可抽奖一次,抽奖方案有两种,顾客只能选择其中的一种.
方案一:从装有10个形状、大小完全相同的小球(其中红球3个,黑球7个)的抽奖盒中,一次性摸出3个球,其中奖规则为:若摸到3个红球,享受免单优惠;若摸出2个红球则打6折,若摸出1个红球,则打7折;若没摸出红球,则不打折.
方案二:从装有10个形状、大小完全相同的小球(其中红球3个,黑球7个)的抽奖盒中,有放回每次摸取1球,连摸3次,每摸到1次红球,立减200元.
(1)若两个顾客均分别消费了600元,且均选择抽奖方案一,试求两位顾客均享受免单优惠的概率;
(2)若某顾客消费恰好满1000元,试从概率的角度比较该顾客选择哪一种抽奖方案更合算?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,函数F(x)=min{2|x1|,x22ax+4a2},
,函数F(x)=min{2|x1|,x22ax+4a2},
其中min{p,q}=![]()
(Ⅰ)求使得等式F(x)=x22ax+4a2成立的x的取值范围;
(Ⅱ)(ⅰ)求F(x)的最小值m(a);
(ⅱ)求F(x)在区间[0,6]上的最大值M(a).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的几何体中,四边形![]() 是菱形,
是菱形,![]() 是矩形,
是矩形,![]() ,
,![]() ,
,![]() ,
, ![]() ,
,![]() 为
为![]() 的中点.
的中点.
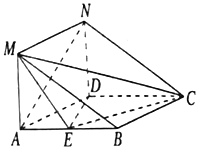
(1)平面![]() 平面
平面![]()
(2)在线段![]() 上是否存在点
上是否存在点![]() ,使二面角
,使二面角![]() 的大小为
的大小为![]() ?若存在,求出
?若存在,求出![]() 的长度;若不存在,请说明理由.
的长度;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com