
如图,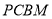 是直角梯形,∠
是直角梯形,∠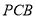 =90°,
=90°,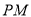 ∥
∥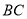 ,
,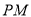 =1,
=1,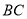 =2,又
=2,又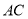 =1,∠
=1,∠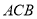 =120°,
=120°,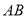 ⊥
⊥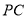 ,直线
,直线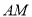 与直线
与直线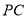 所成的角为60°.
所成的角为60°.
(1)求二面角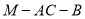 的的余弦值;
的的余弦值;
(2)求点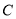 到面
到面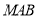 的距离.
的距离.

(1)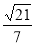 ;(2)
;(2)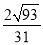 .
.
【解析】
试题分析:此题可用向量法来求解.(1)由题意易知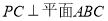 ,则在平面
,则在平面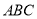 内过点
内过点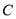 作
作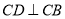 交
交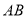 于点
于点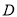 ,分别以
,分别以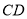 、
、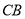 、
、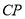 为
为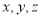 轴,
轴,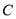 为原点建立空间直角坐标系
为原点建立空间直角坐标系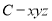 ,找出相应点的坐标,由直线
,找出相应点的坐标,由直线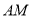 与直线
与直线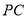 所成角为
所成角为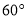 ,求出点
,求出点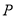 的坐标,从而可确定点
的坐标,从而可确定点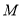 的坐标,由平面
的坐标,由平面 内向量
内向量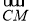 、
、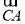 可求得平面平面
可求得平面平面 的法向量
的法向量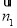 ,平面
,平面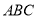 法向量为
法向量为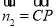 ,根据向量的数量积公式,可求出向量
,根据向量的数量积公式,可求出向量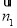 与
与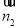 夹角的余弦值,从而求出所求二面角的余弦值;(2)先求出平面
夹角的余弦值,从而求出所求二面角的余弦值;(2)先求出平面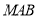 的法向量
的法向量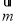 ,又点
,又点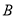 在平面
在平面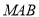 内,可求出向量
内,可求出向量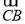 的坐标,由点到平面的向量计算公式
的坐标,由点到平面的向量计算公式 可求得点
可求得点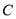 到平面
到平面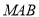 的距离.
的距离.
试题解析:(1)∵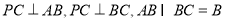 ∴
∴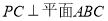 .
.
在平面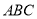 内,过
内,过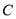 作
作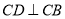 ,建立空间直角坐标系
,建立空间直角坐标系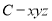 (如图)
(如图)
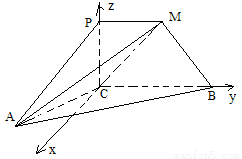
由题意有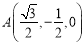 ,设
,设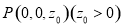 ,
,
则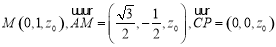
由直线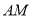 与直线
与直线 所成的解为
所成的解为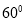 ,得
,得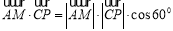 ,
,
即 ,解得
,解得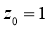
∴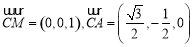 ,设平面
,设平面 的一个法向量为
的一个法向量为 ,
,
则 ,取
,取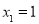 ,得
,得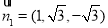 ,平面
,平面 的法向量取为
的法向量取为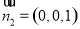
设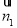 与
与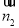 所成的角为
所成的角为 ,则
,则 .
.
显然,二面角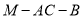 的平面角为锐角,故二面角
的平面角为锐角,故二面角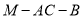 的余弦值为
的余弦值为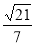 . 5分
. 5分
(2)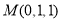 ,
, ,
,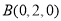 ,
,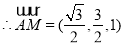 ,
,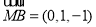 .
.
设平面 的一个法向量
的一个法向量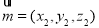 ,则
,则 ,
,
取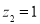 ,得
,得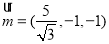 ,则点
,则点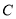 到平面
到平面 的距离
的距离 . 10分
. 10分
考点:1.二面角;2.点到平面距离.


科目:高中数学 来源:2013-2014学年江西省上饶市高三第二次模拟考试理科数学试卷(解析版) 题型:选择题
设等差数列 的前
的前 项和为
项和为 ,且满足
,且满足 ,则
,则 中最大的项为( )
中最大的项为( )
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江西省上饶市高三第二次模拟考试文科数学试卷(解析版) 题型:填空题
某校从参加高三年级期末考试的学生中随机抽取60名学生,将其数学成绩分成六段:[40,50),[50,60), …[90,100),它的频率分布直方图如图所示,则该批学生中成绩不低于60分的人数为___________.
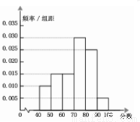
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江西省上饶市高三第二次模拟考试文科数学试卷(解析版) 题型:选择题
设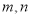 是两条不同的直线,
是两条不同的直线, 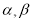 是两个不同的平面,则下列命题正确的是( )
是两个不同的平面,则下列命题正确的是( )
A.若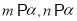 ,则
,则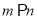 B.若
B.若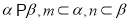 ,则
,则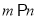
C.若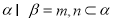 ,则
,则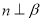 D.若
D.若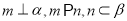 ,则
,则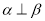
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江苏省高三百校联合调研测试(一)数学试卷(解析版) 题型:解答题
已知函数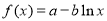 (
(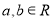 ),其图像在
),其图像在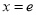 处的切线方程为
处的切线方程为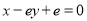 .函数
.函数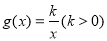 ,
, .
.
(1)求实数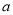 、
、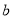 的值;
的值;
(2)以函数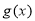 图像上一点为圆心,2为半径作圆
图像上一点为圆心,2为半径作圆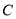 ,若圆
,若圆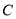 上存在两个不同的点到原点
上存在两个不同的点到原点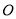 的距离为1,求
的距离为1,求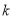 的取值范围;
的取值范围;
(3)求最大的正整数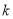 ,对于任意的
,对于任意的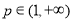 ,存在实数
,存在实数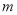 、
、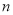 满足
满足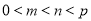 ,使得
,使得 .
.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江苏省高三百校联合调研测试(一)数学试卷(解析版) 题型:填空题
在R上定义运算⊙:a⊙b=ab+2a+b,则不等式x⊙(x-2)<0的解集是 .
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江苏省连云港市高三3月第二次调研考试理科数学试卷(解析版) 题型:解答题
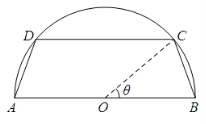
一个圆柱形圆木的底面半径为1m,长为10m,将此圆木沿轴所在的平面剖成两个部分.现要把其中一个部分加工成直四棱柱木梁,长度保持不变,底面为等腰梯形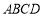 (如图所示,其中O为圆心,
(如图所示,其中O为圆心,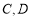 在半圆上),设
在半圆上),设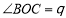 ,木梁的体积为V(单位:m3),表面积为S(单位:m2).
,木梁的体积为V(单位:m3),表面积为S(单位:m2).
(1)求V关于θ的函数表达式;
(2)求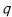 的值,使体积V最大;
的值,使体积V最大;
(3)问当木梁的体积V最大时,其表面积S是否也最大?请说明理由.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江苏省苏锡常镇四市高三教学情况调研二数学试卷(解析版) 题型:填空题
已知△ABC为等腰直角三角形,斜边BC上的中线AD = 2,将△ABC沿AD折成60°的二面角,连结BC,则三棱锥C ? ABD的体积为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com