
((本小题12分)已知函数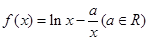 。
。
(1)判断 在定义域上的单调性;
在定义域上的单调性;
(2)若 在
在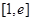 上的最小值为2,求
上的最小值为2,求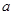 的值。
的值。
解:(1)由题意得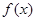 的定义域为
的定义域为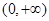 ,
, ……………………(2分)
……………………(2分)
①当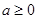 时,
时, ,故
,故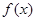 在
在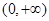 上为增函数…………………………(4分)
上为增函数…………………………(4分)
②当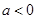 时,由
时,由 得
得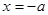 ;由
;由 得
得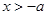 ;
;
由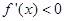 得
得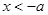 ;
;
∴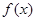 在
在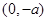 上为减函数;在
上为减函数;在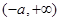 上为增函数. …………………………(6分)
上为增函数. …………………………(6分)
所以,当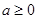 时,
时,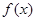 在
在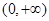 上是增函数;当
上是增函数;当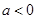 时,
时,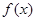 在
在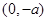 上是减函数,在
上是减函数,在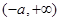 上是增函数…………………………………………………………………………(7分)
上是增函数…………………………………………………………………………(7分)
(2)∵ ,
,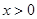 .由(1)可知:
.由(1)可知:
①当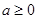 时,
时,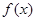 在
在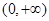 上为增函数,
上为增函数,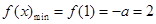 ,得
,得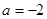 ,矛盾!
,矛盾!
…………………………………………………………………………………………(8分)
②当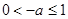 时,即
时,即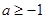 时,
时,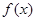 在
在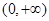 上也是增函数,
上也是增函数,
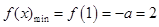 ,∴
,∴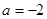 (舍去).………………………………………(9分)
(舍去).………………………………………(9分)
③当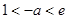 时,即
时,即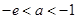 时,
时,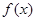 在
在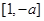 上是减函数,在
上是减函数,在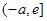 上是增函数,
上是增函数,
∴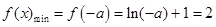 ,得
,得 (舍去). ………………………(10分)
(舍去). ………………………(10分)
④当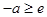 时,即
时,即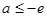 时,
时,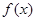 在
在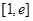 上是减函数,有
上是减函数,有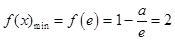 ,
,
∴ …………………………………………………………………………(11分)
…………………………………………………………………………(11分)
综上可知: . ……………………………………………………………………(12分)
. ……………………………………………………………………(12分)
【解析】略


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:高中数学 来源:2010-2011学年福建师大附中高三上学期期中考试理科数学卷 题型:解答题
(本小题12分)已知函数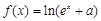 (
( 为常数)是实数集
为常数)是实数集 上的奇函数,函数
上的奇函数,函数 是区间[-1,1]上的减函数.
是区间[-1,1]上的减函数.
(I)求 的值;
的值;
(II)若 在
在 及
及 所在的取值范围上恒成立,求
所在的取值范围上恒成立,求 的取值范围;
的取值范围;
(Ⅲ)讨论关于 的方程
的方程 的根的个数.
的根的个数.
查看答案和解析>>
科目:高中数学 来源:2010年吉林省高一上学期期中考试数学试卷 题型:解答题
(本小题12分)已知二次函数 满足
满足 且
且 .
.
(1)求 的解析式;
的解析式;
(2) 当 时,不等式:
时,不等式: 恒成立,求实数
恒成立,求实数 的范围.
的范围.
(3)设
 ,求
,求 的最大值;
的最大值;
查看答案和解析>>
科目:高中数学 来源:2010-2011年福建省高二下学期期中考试理科数学 题型:解答题
(本小题12分)
已知双曲线的中心在原点,左右焦点分别为 ,离心率为
,离心率为 ,且过点
,且过点 ,
,

(1)求此双曲线的标准方程;
(2)若直线系 (其中
(其中 为参数)所过的定点
为参数)所过的定点 恰在双曲线上,求证:
恰在双曲线上,求证: 。
。
查看答案和解析>>
科目:高中数学 来源:2010-2011年福建省四地六校高二下学期第一次月考数学文卷 题型:解答题
(本小题12分)
已知椭圆C的左右焦点坐标分别是(-1,0),(1, 0),离心率 ,直线
,直线 与椭圆C交于不同的两点M,N,以线段MN为直径作圆P。
与椭圆C交于不同的两点M,N,以线段MN为直径作圆P。
(1)求椭圆C的方程;
(2)若圆P恰过坐标原点,求圆P的方程;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com