Question

（01全国卷） (12分)

设抛物线y² =2px (p＞0)的焦点为F，经过点F的直线交抛物线于A、B两点，点C在抛物线的准线上，且BC∥x轴．证明直线AC经过原点O．

Answer 1

解析：证明一：因为抛物线y² =2px (p＞0)的焦点为F (，0)，所以经过点F的直线的方程可设为

；                        ……4分

代入抛物线方程得

y² －2pmy－p² = 0，

若记A(x₁，y₁)，B(x₂，y₂)，则y₁，y₂是该方程的两个根，所以

y₁y₂ = －p²．                           ……8分

因为BC∥x轴，且点c在准线x = －上，所以点c的坐标为（－，y₂），故直线CO的斜率为

．

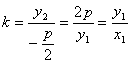即k也是直线OA的斜率，所以直线AC经过原点O．……12分

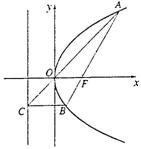
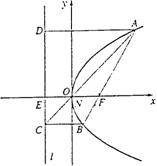
证明二：如图，记x轴与抛物线准线l的交点为E，过A作AD⊥l，D是垂足．则

AD∥FE∥BC．                                                      ……2分

连结AC，与EF相交于点N，则

，

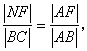                     ……6分

根据抛物线的几何性质，，

，                          ……8分

∴ ，

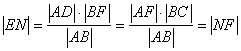即点N是EF的中点，与抛物线的顶点O重合，所以直线AC经过原点O． ……12分