
证明:已知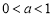 ,则
,则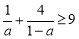
科目:高中数学 来源:2015届浙江省高三上学期第一次统练文科数学试卷(解析版) 题型:解答题
已知函数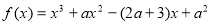 (
(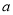 ∈R).
∈R).
(1)若函数 在区间
在区间 上有极小值点,求实数
上有极小值点,求实数 的取值范围;
的取值范围;
(2)若当 时,
时,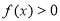 ,求实数
,求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2015届浙江省高二下学期第一次质量检测数学试卷(解析版) 题型:选择题
若集合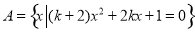 有且仅有2个子集,则实数
有且仅有2个子集,则实数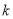 的值是 ( )
的值是 ( )
A.-2 B.-2或-1 C.2或-1 D.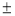 2或-1
2或-1
查看答案和解析>>
科目:高中数学 来源:2015届河南长葛第三实验高中高二下学期第一次考试文数学卷(解析版) 题型:选择题
两个变量 与
与 的回归模型中,分别选择了4个不同模型,它们的相关指数
的回归模型中,分别选择了4个不同模型,它们的相关指数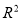 如下,其中拟合效果最好的模型是( )
如下,其中拟合效果最好的模型是( )
(A)模型1的相关指数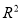 为0.98 (B) 模型2的相关指数
为0.98 (B) 模型2的相关指数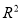 为0.80
为0.80
(C)模型3的相关指数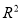 为0.50 (D) 模型4的相关指数
为0.50 (D) 模型4的相关指数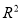 为0.25
为0.25
查看答案和解析>>
科目:高中数学 来源:2015届河南长葛第三实验高中高二下学期第一次考试文数学卷(解析版) 题型:选择题
在独立性检验中,统计量 有两个临界值:3.841和6.635;当
有两个临界值:3.841和6.635;当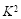 >3.841时,有95%的把握说明两个事件有关,当
>3.841时,有95%的把握说明两个事件有关,当 >6.635时,有99%的把握说明两个事件有关,当
>6.635时,有99%的把握说明两个事件有关,当
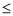 3.841时,认为两个事件无关.在一项打鼾与患心脏病的调查中,共调查了2000人,经计算的
3.841时,认为两个事件无关.在一项打鼾与患心脏病的调查中,共调查了2000人,经计算的 =20. 87,根据这一数据分析,认为打鼾与患心脏病之间
=20. 87,根据这一数据分析,认为打鼾与患心脏病之间
A.有95%的把握认为两者有关
B.约有95%的打鼾者患心脏病
C.有99%的把握认为两者有关
D.约有99%的打鼾者患心脏病
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com