Question

【题目】已知函数 下列四个命题： ①f（f（1））＞f（3）；
②x0∈（1，+∞）， ；
③f（x）的极大值点为x=1；
④x1 ， x2∈（0，+∞），|f（x1）﹣f（x2）|≤1
其中正确的有 ． （写出所有正确命题的序号）

Answer 1

【答案】①②③④
【解析】解：函数f（x）的图形如图所示，

对于①，f（1）=2，f（f（1））=f（2）= ，f（3）= ，故①正确．

对于②，x＞1时，f′（x）=﹣ =﹣ ，x= ．故②正确．

对于③，根据图形可判断③正确．

对于④，x∈（0，+∞）时，1＜f（x）≤2，

∴x1，x2∈（0，+∞），|f（x1）﹣f（x2）|≤1正确

故答案为：①②③④

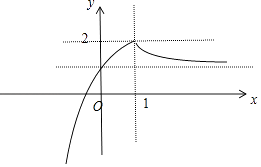
解：函数f（x）的图形如图所示，

对于①，f（1）=2，f（f（1））=f（2）= ，f（3）= ，．

对于②，x＞1时，f′（x）=﹣ =﹣ ，x= ．．

对于③，根据图形可判断．

对于④，由x∈（0，+∞）时，1＜f（x）≤2，可判断