
【题目】已知函数![]() ,
, ![]() .
.
(1)若![]() ,求函数
,求函数![]() 的单调递减区间;
的单调递减区间;
(2)若关于![]() 的不等式
的不等式![]() 恒成立,求整数
恒成立,求整数![]() 的最小值;
的最小值;
(3)若![]() ,正实数
,正实数![]() ,
, ![]() 满足
满足![]() ,证明:
,证明: ![]() .
.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)证明见解析.
;(3)证明见解析.
【解析】试题分析:(1)由![]() 求出
求出![]() 的值,再利用导数求出函数
的值,再利用导数求出函数![]() 的单调递减区间;(2)分离出变量
的单调递减区间;(2)分离出变量 ,令
,令 ,只要
,只要![]() ,利用导数求出令
,利用导数求出令![]() 的最大值即可;(3)由
的最大值即可;(3)由![]() ,即
,即![]() ,令
,令![]() ,则由
,则由![]() ,利用导数法求得
,利用导数法求得![]() ,从而可得所以
,从而可得所以![]() ,解得即可.
,解得即可.
试题解析:
(1)因为![]() ,所以
,所以![]() ,
,
此时![]() ,
, ![]() ,
,
![]() ,
,
由![]() ,得
,得![]() ,又
,又![]() ,所以
,所以![]() ,
,
所以![]() 的单调减区间为
的单调减区间为![]() .
.
(2)由![]() 恒成立,得
恒成立,得![]() 在
在![]() 上恒成立,
上恒成立,
问题等价于 在
在![]() 上恒成立,
上恒成立,
令 ,只要
,只要![]() ,
,
因为 ,令
,令![]() ,得
,得![]() .
.
设![]() ,因为
,因为![]() ,所以
,所以![]() 在
在![]() 上单调递减,
上单调递减,
不妨设![]() 的根为
的根为![]() ,
,
当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() ,
,
所以![]() 在
在![]() 上是增函数,在
上是增函数,在![]() 上是减函数,
上是减函数,
所以![]()
 ,
,
因为![]() ,
, ![]() ,
,
所以![]() ,此时
,此时![]() ,即
,即![]() ,
,
所以![]() ,即整数
,即整数![]() 的最小值为2.
的最小值为2.
(3)当![]() 时,
时, ![]() ,
,
由![]() ,即
,即![]() ,
,
从而![]() ,
,
令![]() ,则由
,则由![]() ,得
,得![]() ,
,
可知, ![]() 在区间
在区间![]() 上单调递减,在区间
上单调递减,在区间![]() 上单调递增,所以
上单调递增,所以![]() ,
,
所以![]() ,因此
,因此![]() 成立.
成立.


科目:高中数学 来源: 题型:
【题目】现有![]() 六支足球队参加单循环比赛(即任意两支球队只踢一场比赛),第一周的比赛中
六支足球队参加单循环比赛(即任意两支球队只踢一场比赛),第一周的比赛中![]() ,各踢了
,各踢了![]() 场,
场, ![]() 各踢了
各踢了![]() 场,
场, ![]() 踢了
踢了![]() 场,且
场,且![]() 队与
队与![]() 队未踢过,
队未踢过, ![]() 队与
队与![]() 队也未踢过,则在第一周的比赛中,
队也未踢过,则在第一周的比赛中, ![]() 队踢的比赛的场数是( )
队踢的比赛的场数是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() 的渐近线方程是
的渐近线方程是![]() ,右焦点
,右焦点![]() ,则双曲线
,则双曲线![]() 的方程为_________,又若点
的方程为_________,又若点![]() ,
, ![]() 是双曲线
是双曲线![]() 的左支上一点,则
的左支上一点,则![]() 周长的最小值为__________.
周长的最小值为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[2018·赣中联考]李冶(1192-1279),真实栾城(今属河北石家庄市)人,金元时期的数学家、诗人,晚年在封龙山隐居讲学,数学著作多部,其中《益古演段》主要研究平面图形问题:求圆的直径、正方形的边长等.其中一问:现有正方形方田一块,内部有一个圆形水池,其中水池的边缘与方田四边之间的面积为13.75亩,若方田的四边到水池的最近距离均为二十步,则圆池直径和方田的边长分别是(注:240平方步为1亩,圆周率按3近似计算)( )
A. 10步,50步 B. 20步,60步 C. 30步,70步 D. 40步,80步
查看答案和解析>>
科目:高中数学 来源: 题型:
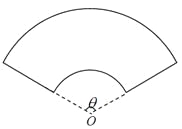
【题目】某单位拟建一个扇环面形状的花坛(如图所示),该扇环面是由以点![]() 为圆心的两个同心圆弧和延长后通过点
为圆心的两个同心圆弧和延长后通过点![]() 的两条直线段围成.按设计要求扇环面的周长为30米,其中大圆弧所在圆的半径为10米.设小圆弧所在圆的半径为
的两条直线段围成.按设计要求扇环面的周长为30米,其中大圆弧所在圆的半径为10米.设小圆弧所在圆的半径为![]() 米,圆心角为
米,圆心角为![]() (弧度).
(弧度).
(1)求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)已知在花坛的边缘(实线部分)进行装饰时,直线部分的装饰费用为4元/米,弧线部分的装饰费用为9元/米.设花坛的面积与装饰总费用的比为![]() ,求
,求![]() 关于
关于![]() 的函数关系式,并求出
的函数关系式,并求出![]() 为何值时,
为何值时, ![]() 取得最大值?
取得最大值?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() (
(![]() 为常数).
为常数).
(1)若函数![]() 与函数
与函数![]() 在
在![]() 处有相同的切线,求实数
处有相同的切线,求实数![]() 的值;
的值;
(2)若![]() ,且
,且![]() ,证明:
,证明: ![]() ;
;
(3)若对任意![]() ,不等式恒
,不等式恒![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马;将四个面都为直角三角形的三棱锥称之为鳖臑。若三棱锥P-ABC为鳖臑,PA⊥面ABC,PA=AB=2,AC=4,三棱锥P-ABC的四个顶点都在球的球面上,则球0的表面积为( )
A. 8πB. 12πC. 20πD. 24π
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com