
【题目】已知函数f(x)是定义域在R上的奇函数,当x>0时,f(x)=x2﹣2x.
(1)求出函数f(x)在R上的解析式;
(2)写出函数的单调区间.
【答案】(1)f(x)=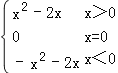 ;
;
(2)则函数的单调递增区间为为[1,+∞),(﹣∞,﹣1],函数的单调递减区间为为[﹣1,1].
【解析】
试题(1)根据函数f(x)为定义域为R的奇函数,当x>0时,f(x)=x2﹣2x,我们根据定义域为R的奇函数的图象必过原点,则f(﹣x)=﹣f(x),即可求出函数f(x)在R上的解析式;
(2)根据(1)中分段函数的解析式,我们易画出函数f(x)的图象,利用数形结合进行求解即可.
解:(1)∵函数f(x)是定义域在R上的奇函数,
∴当x=0时,f(0)=0;
当x<0时,﹣x>0,则f(﹣x)=x2+2x.
∵f(x)是奇函数,
∴f(﹣x)=﹣f(x)
∴f(﹣x)=x2+2x=﹣f(x),
即f(x)=﹣x2﹣2x.
综上:f(x)=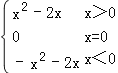 .
.
(2)函数f(x)=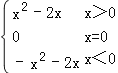 的图象如下图所示:
的图象如下图所示:
则函数的单调递增区间为为[1,+∞),(﹣∞,﹣1],
函数的单调递减区间为为[﹣1,1].
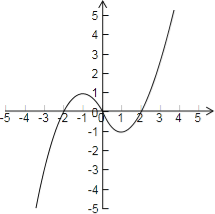


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:高中数学 来源: 题型:
【题目】函数![]() 的图象为
的图象为![]() ,则以下结论中正确的是__________.(写出所有正确结论的编号)
,则以下结论中正确的是__________.(写出所有正确结论的编号)
①图象![]() 关于直线
关于直线![]() 对称;
对称;
②图象![]() 关于点
关于点![]() 对称;
对称;
③函数![]() 在区间
在区间![]() 内是增函数;
内是增函数;
④由![]() 的图象向右平移
的图象向右平移![]() 个单位长度可以得到图象
个单位长度可以得到图象![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】由实数组成的集合A具有如下性质:若![]() ,
,![]() 且
且![]() ,那么
,那么![]() .
.
(1)试问集合A能否恰有两个元素且![]() ?若能,求出所有满足条件的集合A;若不能,请说明理由;
?若能,求出所有满足条件的集合A;若不能,请说明理由;
(2)是否存在一个含有元素0的三元素集合A;若存在请求出集合,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】 如图是正方体的平面展开图.在这个正方体中,
①BM∥平面DE;②CN∥平面AF;③平面BDM∥平面AFN;④平面BDE∥平面NCF.
以上四个命题中,正确命题的序号是________.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司在甲、乙两地销售某种品牌车,利润(单位:万元)分别为![]() 和
和![]() ,其中
,其中![]() 为销售量(单位:辆)
为销售量(单位:辆)
(1)当销售量在什么范围时,甲地的销售利润不低于乙地的销售利润;
(2)若该公司在这两地共销售![]() 辆车,则甲、乙两地各销售多少量时?该公司能获得利润
辆车,则甲、乙两地各销售多少量时?该公司能获得利润![]() 最大,最大利润是多少?
最大,最大利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列关于相关系数![]() 的说法不正确的是( )
的说法不正确的是( )
A. 相关系数![]() 越大两个变量间相关性越强;
越大两个变量间相关性越强;
B. 相关系数![]() 的取值范围为
的取值范围为![]() ;
;
C. 相关系数![]() 时两个变量正相关,
时两个变量正相关,![]() 时两个变量负相关;
时两个变量负相关;
D. 相关系数![]() 时,样本点在同一直线上。
时,样本点在同一直线上。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com