Question

【题目】在四棱锥PABCD中，底面ABCD是正方形，侧棱PD垂直于底面ABCD，PD＝DC，点E是PC的中点．

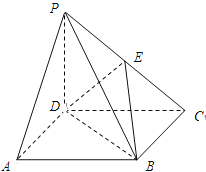
（Ⅰ）求证：PA∥平面EBD；

（Ⅱ）求二面角EBDP的余弦值．

Answer 1

【答案】（Ⅰ）详见解析；（Ⅱ）.

【解析】

试题分析：（Ⅰ）几何法：连接,连接,根据线面平行的判定定理可先证明线线平行，即证明；向量法：以点D为原点，DA为x轴，DC为y轴，DP为z轴建立直角坐标系，求平面的法向量，若，说明与法向量垂直，即与平面平行；

（Ⅱ）向量法求二面角的余弦值，即先求两个平面的法向量，而平面的法向量就是,即求.

试题解析：解：(Ⅰ)法一：以点D为原点，DA为x轴，DC为y轴，DP为z轴建立直角坐标系，设正方形的边长为1，则

∴,．

设平面EBD的法向量为，

可求得,∴,∴∥平面EBD．

即PA∥平面EBD．

法二：连接AC，设AC∩BD＝O，连接OE，则OE∥PA，∴PA∥平面EBD.

(Ⅱ)设平面PBD的法向量为．

∴，∴二面角E-BD-P的平面角的余弦值为.