
分析 (1)利用向量的数量积公式,化简函数,结合f(x)=1,利用二倍角公式求cos(x+$\frac{π}{3}$)的值;
(2)先求出$B=\frac{π}{3}$,可得$0<A<\frac{2π}{3}$,$\frac{π}{6}<\frac{A}{2}+\frac{π}{6}<\frac{π}{2}$,$\frac{1}{2}<sin(\frac{A}{2}+\frac{π}{6})<1$,即可求出函数f(A)的取值范围.
解答 解:(1)$f(x)=\overrightarrow m•\overrightarrow n=\sqrt{3}sin\frac{x}{4}•cos\frac{x}{4}+{cos^2}\frac{x}{4}$…(1分)
=$\frac{{\sqrt{3}}}{2}sin\frac{x}{2}+\frac{{1+cos\frac{x}{2}}}{2}$…2分
=$\frac{{\sqrt{3}}}{2}sin\frac{x}{2}+\frac{1}{2}cos\frac{x}{2}+\frac{1}{2}=sin(\frac{x}{2}+\frac{π}{6})+\frac{1}{2}$…(3分)
∵f(x)=1,
∴$sin(\frac{x}{2}+\frac{π}{6})+\frac{1}{2}=1$…(4分)
∴$cos(x+\frac{π}{3})=1-2{sin^2}(\frac{x}{2}+\frac{π}{6})=1-2×\frac{1}{4}=\frac{1}{2}$.…(6分)
(2)∵(2a-c)cosB=bcosC,
∴由正弦定理得(2sinA-sinC)cosB=sinBcosC…(8分)
∴2sinAcosB-sinCcosB=sinBcosC,
∴2sinAcosB=sin(B+C),…(9分)
∵A+B+C=π,∴sin(B+C)=sinA且sinA≠0,
∴$cosB=\frac{1}{2}$,
又B∈(0,π),∴$B=\frac{π}{3}$…(10分)
∴$0<A<\frac{2π}{3}$,∴$\frac{π}{6}<\frac{A}{2}+\frac{π}{6}<\frac{π}{2}$,
∴$\frac{1}{2}<sin(\frac{A}{2}+\frac{π}{6})<1$;
又∵$f(x)=sin(\frac{x}{2}+\frac{π}{6})+\frac{1}{2}$,∴$f(A)=sin(\frac{A}{2}+\frac{π}{6})+\frac{1}{2}$,
故函数f(A)的取值范围是$(1,\frac{3}{2})$.…(12分)
点评 本题考查向量的数量积公式的运用,考查三角函数的化简,考查正弦定理,属于中档题.


科目:高中数学 来源: 题型:选择题
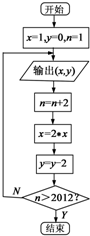 某程序框图如图所示,现将输出(x,y)值依次记为:(x1,y1),(x2,y2),…,(xn,yn)…若程序运行中输出的一个数组是(x,-10)则数组中的x=( )
某程序框图如图所示,现将输出(x,y)值依次记为:(x1,y1),(x2,y2),…,(xn,yn)…若程序运行中输出的一个数组是(x,-10)则数组中的x=( )| A. | 32 | B. | 24 | C. | 18 | D. | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-4)∪[-3,3) | B. | (-4,-3]∪{1}∪(3,+∞) | C. | (-∞,-3]∪{1}∪(3,+∞) | D. | [-3,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com